题目内容
11．
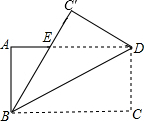如图，将矩形ABCD沿对角线BD折叠，使点C与C′重合．若AB=3，则C′D的长为3．
分析 根据矩形的对边相等可得CD=AB，再根据翻折变换的性质可得C′D=CD，代入数据即可得解．
解答 解：在矩形ABCD中，CD=AB，
∵矩形ABCD沿对角线BD折叠后点C和点C′重合，
∴C′D=CD，
∴C′D=AB，
∵AB=3，
∴C′D=3．
故答案为3．
点评 本题考查了矩形的对边相等的性质，翻折变换的性质，是基础题，熟记性质是解题的关键．
练习册系列答案
相关题目
如图是由4个完全相同的小正方形组成的几何体，这个几何体的主视图是（ ）
已知二次函数y=-x2+2x+m．
16．
如图，△ABE和△CDE是以点E为位似中心的位似图形，已知点A（3，4），点C（2，2），点D（3，1），则点D的对应点B的坐标是（ ）
如图，△ABE和△CDE是以点E为位似中心的位似图形，已知点A（3，4），点C（2，2），点D（3，1），则点D的对应点B的坐标是（ ）| A． | （4，2） | B． | （4，1） | C． | （5，2） | D． | （5，1） |
1．甲、乙两人练习跑步，若乙先跑8米，则甲跑4分钟可追上乙；若乙先跑2分钟，则甲跑5分钟可追上乙．若设甲的速度为x米/分，乙的速度为y米/分，则下列列出的方程组中正确的是（ ）
| A． | $\left\{\begin{array}{l}{4x=4y+8}\\{5x=2y+5y}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{4x+8=4y}\\{5x=2y+5y}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{4x=4y+8}\\{5x=5y-2y}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{4x+8=4y}\\{5x+2y=5y}\end{array}\right.$ |