题目内容
12.在$\sqrt{8}$,$\sqrt{12}$,$\sqrt{27}$,$\sqrt{18}$中与$\sqrt{3}$是同类二次根式的是$\sqrt{12}$,$\sqrt{27}$.分析 根据同类二次根式的定义解答即可.
解答 解:$\sqrt{8}$=2$\sqrt{2}$,被开方数是2,与$\sqrt{3}$不是同类二次根式.
$\sqrt{12}$=2$\sqrt{3}$,被开方数是3,与$\sqrt{3}$是同类二次根式.
$\sqrt{27}$=3$\sqrt{3}$,被开方数是3,与$\sqrt{3}$是同类二次根式.
$\sqrt{18}$=3$\sqrt{2}$,被开方数是2,与$\sqrt{3}$不是同类二次根式.
综上所述,与$\sqrt{3}$是同类二次根式的是:$\sqrt{12}$,$\sqrt{27}$.
故答案是:$\sqrt{12}$,$\sqrt{27}$.
点评 此题主要考查了同类二次根式的定义,即化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式.

练习册系列答案
相关题目
17.不等式2+x<1的解是( )
| A. | x>1 | B. | x>-1 | C. | x<1 | D. | x<-1 |
1.甲、乙两人练习跑步,若乙先跑8米,则甲跑4分钟可追上乙;若乙先跑2分钟,则甲跑5分钟可追上乙.若设甲的速度为x米/分,乙的速度为y米/分,则下列列出的方程组中正确的是( )
| A. | $\left\{\begin{array}{l}{4x=4y+8}\\{5x=2y+5y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{4x+8=4y}\\{5x=2y+5y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{4x=4y+8}\\{5x=5y-2y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{4x+8=4y}\\{5x+2y=5y}\end{array}\right.$ |
2.以下是甲、乙、丙三人看地图时对四个坐标的描述:
甲:从学校向北直走500米,再向东直走100米可到图书馆.
乙:从学校向西直走300米,再向北直走200米可到邮局.
丙:邮局在火车站西200米处.
根据三人的描述,若从图书馆出发,判断下列哪一种走法,其终点是火车站( )
甲:从学校向北直走500米,再向东直走100米可到图书馆.
乙:从学校向西直走300米,再向北直走200米可到邮局.
丙:邮局在火车站西200米处.
根据三人的描述,若从图书馆出发,判断下列哪一种走法,其终点是火车站( )
| A. | 向南直走300米,再向西直走200米 | B. | 向南直走300米,再向西直走100米 | ||
| C. | 向南直走700米,再向西直走200米 | D. | 向南直走700米,再向西直走600米 |
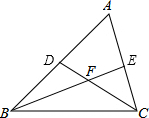 如图,在△ABC中,D是AB上一点,E是AC上一点,BE、CD相交于点F,∠A=70°,∠ACD=30°,∠ABE=25°.求:
如图,在△ABC中,D是AB上一点,E是AC上一点,BE、CD相交于点F,∠A=70°,∠ACD=30°,∠ABE=25°.求: