题目内容
12.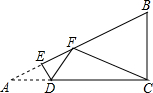 如图,有一直角三角形纸片ACB,∠A=30°,∠ACB=90°,BC=2,点D是AC边上一动点.过点D沿直线DE方向折叠三角形纸片,使点A落在射线AB上的点F处,当以点F、B、C为顶点的三角形为等腰三角形时,AD的长为$\frac{2\sqrt{3}}{3}$.
如图,有一直角三角形纸片ACB,∠A=30°,∠ACB=90°,BC=2,点D是AC边上一动点.过点D沿直线DE方向折叠三角形纸片,使点A落在射线AB上的点F处,当以点F、B、C为顶点的三角形为等腰三角形时,AD的长为$\frac{2\sqrt{3}}{3}$.
分析 根据直角三角形的性质可知∠B=60°,所以当以点F、B、C为顶点的三角形为等腰三角形时,则△FBC是等边三角形,设AE=x,则EF=x,BF=4-2x,若BF=BC,则4-2x=2,解方程即可.
解答 解:由翻折变换的性质得:AE=EF,
∵∠A=30°,∠ACB=90°,BC=2,
∴AB=4,∠B=60°,
设AE=EF=x,则BF=4-2x;
当以点F、B、C为顶点的三角形为等腰三角形时,则△FBC是等边三角形,
若BF=BC,则4-2x=2,
解得:x=1,
∵∠A=30°,
∴AD=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了翻折变换的性质、等边三角形的判定与性质、锐角三角函数;本题的关键是发现△FBC是等边三角形,不需分类讨论.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 E是正方形ABCD的对角线BD上一点,EF⊥BC,EG⊥CD,垂足分别是F、G.求证:
E是正方形ABCD的对角线BD上一点,EF⊥BC,EG⊥CD,垂足分别是F、G.求证: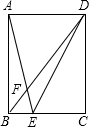 如图,在矩形ABCD中,AB=12,AD=9,点E是边BC上一点,连接AE,BD相交于点F,连接DE,若sin∠DEC=$\frac{2\sqrt{5}}{5}$,则BF=$\frac{15}{4}$.
如图,在矩形ABCD中,AB=12,AD=9,点E是边BC上一点,连接AE,BD相交于点F,连接DE,若sin∠DEC=$\frac{2\sqrt{5}}{5}$,则BF=$\frac{15}{4}$.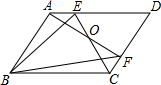 如图,在?ABCD中.E,F分别是AD,CD上,AF与CE交于点O,有下列命题:
如图,在?ABCD中.E,F分别是AD,CD上,AF与CE交于点O,有下列命题: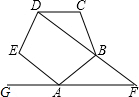 如图,已知正五边形ABCDE,过点A作直线AF∥CD,交DB的延长线于点F
如图,已知正五边形ABCDE,过点A作直线AF∥CD,交DB的延长线于点F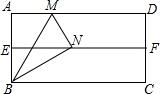 数学兴趣小组开展以下折纸活动:
数学兴趣小组开展以下折纸活动: