题目内容
11.已知抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,则△ABC的面积是6.分析 求出A、B、C三点的坐标,然后利用三角形面积公式即可求出答案.
解答 解:令y=0代入y=-x2+2x+3,
∴-x2+2x+3=0,
解得:x=-1或x=3,
∴A(-1,0),B(3,0),
∴AB=4,
令x=0代入y=-x2+2x+3,
∴y=3,
∴C(0,3)
∴OC=3,
∴△ABC的面积为:$\frac{1}{2}$AB•OC=$\frac{1}{2}$×4×3=6,
故答案为:6,
点评 本题考查抛物线与x轴的交点坐标问题,解题的关键是利用一元二次方程的解法求出抛物线与x轴的交点坐标,本题属于基础题型.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
19.已知P=-2a-1,Q=a+1且2P-Q=0,则a的值为( )
| A. | 2 | B. | 1 | C. | -0.6 | D. | -1 |
3.若反比例函数y=$\frac{2k-1}{x}$的图象经过第二、四象限,则k的取值范围是( )
| A. | k>$\frac{1}{2}$ | B. | k<$\frac{1}{2}$ | C. | k=$\frac{1}{2}$ | D. | k≤$\frac{1}{2}$ |
20.下列大小比较正确的是( )
| A. | $\sqrt{2}$>$\sqrt{3}$ | B. | 2<$\sqrt{5}$ | C. | 2$\sqrt{2}$<$\sqrt{5}$ | D. | 0<-$\sqrt{2}$ |
 如图所示,直线m是一次函数y=kx+b的图象.
如图所示,直线m是一次函数y=kx+b的图象.
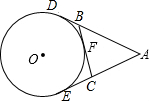 如图,AE,AD,BC分别切⊙O于点E、D和点F,若AD=8cm,则△ABC的周长为16cm.
如图,AE,AD,BC分别切⊙O于点E、D和点F,若AD=8cm,则△ABC的周长为16cm.