题目内容
6.点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第三象限内的概率是$\frac{1}{10}$.分析 先画树状图展示所有20种等可能的结果数,再根据第三象限点的坐标特征找出点P(a,b)在平面直角坐标系中第三象限内的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有20种等可能的结果数,其中点P(a,b)在平面直角坐标系中第三象限内的结果数为2,
所以点P(a,b)在平面直角坐标系中第三象限内的概率=$\frac{2}{20}$=$\frac{1}{10}$,
故答案为:$\frac{1}{10}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了坐标确定位置.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.某乒乓球馆有两种计费方案,如下图表.李强和同学们打算周末去此乒乓球馆连续打球4小时,经服务生测算后,告知他们包场计费方案会比人数计费方案便宜,则他们参与包场的人数至少为( )
| 包场计费:包场每场每小时50元,每人须另付入场费5元 |
| 人数计费:每人打球2小时20元,接着续打球每人每小时6元 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
11.某商人将单价为8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价(为偶数)提高( )
| A. | 8元或10元 | B. | 12元 | C. | 8元 | D. | 10元 |
18.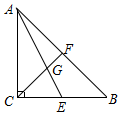 如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )
如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )
 如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )
如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{13}$ |
6.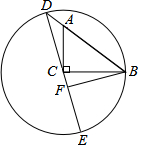 如图,直角△ABC中,∠ACB=90°,AC=3,BC=4,以C为圆心BC为半径画圆交BA延长线于点D,连接DC并延长交圆C于点E,过点B作DE的垂线BF,垂足为点F,那么线段BF的长度为( )
如图,直角△ABC中,∠ACB=90°,AC=3,BC=4,以C为圆心BC为半径画圆交BA延长线于点D,连接DC并延长交圆C于点E,过点B作DE的垂线BF,垂足为点F,那么线段BF的长度为( )
 如图,直角△ABC中,∠ACB=90°,AC=3,BC=4,以C为圆心BC为半径画圆交BA延长线于点D,连接DC并延长交圆C于点E,过点B作DE的垂线BF,垂足为点F,那么线段BF的长度为( )
如图,直角△ABC中,∠ACB=90°,AC=3,BC=4,以C为圆心BC为半径画圆交BA延长线于点D,连接DC并延长交圆C于点E,过点B作DE的垂线BF,垂足为点F,那么线段BF的长度为( )| A. | $\frac{18}{5}$ | B. | 3.5 | C. | $\frac{19}{5}$ | D. | $\frac{96}{25}$ |
 如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的图形的周长是210cm.
如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的图形的周长是210cm.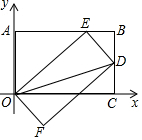 将矩形OABC如图放置在平面直角坐标系中,若OA=6,AB=10,点D为BC上一点,将矩形OABC沿OD折叠使得点C恰好落在AB边上的点E处.
将矩形OABC如图放置在平面直角坐标系中,若OA=6,AB=10,点D为BC上一点,将矩形OABC沿OD折叠使得点C恰好落在AB边上的点E处.