题目内容
16.求y=$\sqrt{{x}^{2}-2x+3}$(-2≤x≤2)的最小值和最大值.分析 因为y=$\sqrt{{x}^{2}-2x+3}$=$\sqrt{(x-1)^{2}+2}$,设y′=(x-1)2+2利用函数y′在-2≤x≤2的最大值,最小值解决问题.
解答 解:y=$\sqrt{{x}^{2}-2x+3}$=$\sqrt{(x-1)^{2}+2}$,
设y′=(x-1)2+2,
∵当-2≤x≤2时,11≥y′≥2,
∴y的最大值,是$\sqrt{11}$,y的最小值是$\sqrt{2}$.
点评 本题考查二次函数的最值问题,解题的注意点是注意自变量x的取值范围(要考虑端点取值),属于中考常考题型.

练习册系列答案
相关题目
3.设$6-\sqrt{13}$的整数部分为a,小数部分为b,那么2a-b的值是( )
| A. | $3-\sqrt{3}$ | B. | $4-\sqrt{13}$ | C. | $\sqrt{13}$ | D. | $4+\sqrt{13}$ |
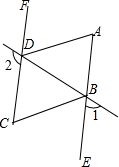 如图,已知∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
如图,已知∠1+∠2=180°,∠A=∠C,DA平分∠BDF.