题目内容
10.计算(1)-4$\frac{2}{3}$-(-3$\frac{1}{3}$)-(-6$\frac{1}{2}$)+(-2$\frac{1}{4}$)
(2)1-(-$\frac{1}{24}$)+($\frac{2}{3}$-$\frac{3}{4}$+$\frac{7}{8}$)
(3)已知A,B关于x的多项式,且A=x2-2x+1,A-B=2x2-6x+3,求A+B.
(4)先化简,再求值:$\frac{1}{4}$(-4x2+2x-8y)-(-x-2y),其中x=$\frac{1}{2}$,y=2015.
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式利用减法法则变形,计算即可得到结果;
(3)把A与B代入A+B中,去括号合并即可得到结果;
(4)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.
解答 解:(1)原式=-4$\frac{2}{3}$+3$\frac{1}{3}$+6$\frac{1}{2}$-2$\frac{1}{4}$=-1$\frac{1}{3}$+4$\frac{1}{4}$=2$\frac{11}{12}$;
(2)原式=1+$\frac{1}{24}$+$\frac{2}{3}$-$\frac{3}{4}$+$\frac{7}{8}$=1$\frac{19}{24}$;
(3)∵A=x2-2x+1,A-B=2x2-6x+3,
∴A+B=x2-2x+1+2x2-6x+3=3x2-8x+4;
(4)原式=-x2+$\frac{1}{2}$x-2y+x+2y=-x2+$\frac{3}{2}$x,
当x=$\frac{1}{2}$时,原式=$\frac{1}{2}$.
点评 此题考查了整式的加减-化简求值,以及有理数的加减混合运算,熟练掌握去括号法则与合并同类项法则是解本题的关键.

练习册系列答案
相关题目
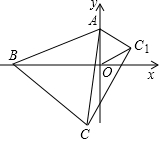 如图,在平面直角坐标系中,点A的坐标是(0,2),点B从坐标原点O出发,沿x轴负半轴运动,以AB为边作等边三角形ABC(A,B,C按逆时针顺序排列),当点B在原点O时,记此时的等边三角形为△AOC1.
如图,在平面直角坐标系中,点A的坐标是(0,2),点B从坐标原点O出发,沿x轴负半轴运动,以AB为边作等边三角形ABC(A,B,C按逆时针顺序排列),当点B在原点O时,记此时的等边三角形为△AOC1. 如图,点E为BC的中点,若∠B=∠AEF=∠C=90°.连接AF
如图,点E为BC的中点,若∠B=∠AEF=∠C=90°.连接AF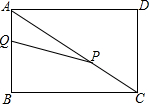 如图,在矩形ABCD中.AB=3cm.Bc=4cm.动点P以2cm/秒的速度从点C出发,沿CA向点A移动.同时动点Q以1cm/秒的速度从点A出发沿AB向点B移动.设P、Q两点移动t秒.
如图,在矩形ABCD中.AB=3cm.Bc=4cm.动点P以2cm/秒的速度从点C出发,沿CA向点A移动.同时动点Q以1cm/秒的速度从点A出发沿AB向点B移动.设P、Q两点移动t秒.