题目内容
15．
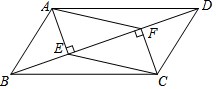如图，在平行四边形ABCD中，连接对角线BD，过A，C两点分别作AE⊥BD，CF⊥BD，E，F为垂足，求证：四边形AECF是平行四边形．
分析 首先真证明△ABE≌△CDF，然后根据一组对边平行且相等的四边形是平行四边形判定．
解答 证明：∵平行四边形ABCD中，AB∥CD，且AB=CD．
∴∠ABE=∠CDF，
∴在△ABE和△CDF中，
$\left\{\begin{array}{l}{∠ABE=∠CDF}\\{∠AEB=∠CFD}\\{AB=CD}\end{array}\right.$，
∴△ABE≌△CDF，
∴AE=CF，
又∵AE⊥BD，CF⊥BD，
∴AE∥CF，
∴四边形AECF是平行四边形．
点评 本题考查了平行四边形的判定与性质，以及全等三角形的判定，证明AE=CF是关键．
练习册系列答案
相关题目
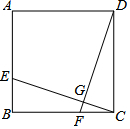如图，点E，F分别在正方形ABCD的边AB，BC上，且EC⊥DF，垂足为G，若AE=2，BE=1，求DF的长．
如图，点E、F分别在正方形ABCD的边BC、CD上，且BE=CF．