题目内容
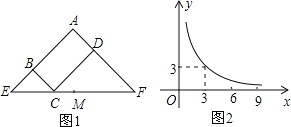
【题目】如图,![]() 中,
中,![]() ,
,![]() ,面积为150.
,面积为150.

(1)尺规作图:作![]() 的平分线交
的平分线交![]() 于点
于点![]() ;(不要求写作法,保留作图痕迹)
;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,求出点![]() 到两条直角边的距离.
到两条直角边的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用尺规作图的步骤作出∠ACB的平分线交AB于点D即可;
(2)作![]() 于E,
于E,![]() 于F,根据面积求出BC的长.法一:根据角平分线的性质得出DE=DF,从而得出四边形CEDF为正方形.再由
于F,根据面积求出BC的长.法一:根据角平分线的性质得出DE=DF,从而得出四边形CEDF为正方形.再由![]() ,得出
,得出![]() ,列方程可以求出结果;法二:根据
,列方程可以求出结果;法二:根据![]() ,利用面积法可求得DE,DF的值.
,利用面积法可求得DE,DF的值.
解:(1)∠ACB的平分线CD如图所示:

(2)已知![]() ,面积为150,∴
,面积为150,∴![]() .
.
法一:作![]() ,
,![]() ,
,

∵![]() 是
是![]() 角平分线,
角平分线,
∴![]() ,
,![]() ,而
,而![]() ,
,
∴四边形![]() 为正方形.
为正方形.
设![]() 为
为![]() ,则由
,则由![]() ,
,
∴![]() ,∴
,∴![]() .
.
即![]() ,得
,得![]() .
.
∴点![]() 到两条直角边的距离为
到两条直角边的距离为![]() .
.
法二:![]() ,
,
即![]() ,
,
又由(1)知AC=15,BC=20,
∴![]() ,
,
∴![]() .
.
故点![]() 到两条直角边的距离为
到两条直角边的距离为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】装潢公司要给边长为6米的正方形墙面ABCD进行装潢,设计图案如图所示(四周是四个全等的矩形,用材料甲进行装潢;中心区是正方形MNPQ,用材料乙进行装潢).
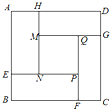
两种装潢材料的成本如下表:
材料 | 甲 | 乙 |
价格(元/米2) | 50 | 40 |
设矩形的较短边AH的长为x米,装潢材料的总费用为y元.
(1)MQ的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于2米时,预备资金1760元购买材料一定够用吗?请说明理由.