Question

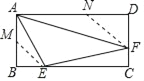
【题目】如图，在矩形ABCD中，AB=2，BC=4，点E、F分别在BC、CD上，若AE=，∠EAF=45°，则AF的长为_____．

Answer 1

【答案】

【解析】取AB的中点M，连接ME，在AD上截取ND=DF，设DF=DN=x，则NF=x，再利用矩形的性质和已知条件证明△AME∽△FNA，利用相似三角形的性质：对应边的比值相等可求出x的值，在直角三角形ADF中利用勾股定理即可求出AF的长．

取AB的中点M，连接ME，在AD上截取ND=DF，设DF=DN=x，

∵四边形ABCD是矩形，

∴∠D=∠BAD=∠B=90°，AD=BC=4，

∴NF=x，AN=4﹣x，

∵AB=2，

∴AM=BM=1，

∵AE=，AB=2，

∴BE=1，

∴ME=，

∵∠EAF=45°，

∴∠MAE+∠NAF=45°，

∵∠MAE+∠AEM=45°，

∴∠MEA=∠NAF，

∴△AME∽△FNA，

∴，

∴，

解得：x=

∴AF=

故答案为：．