Question

【题目】在正方形中，点是直线上动点，以为边作正方形，所在直线与所在直线交于点，连接．

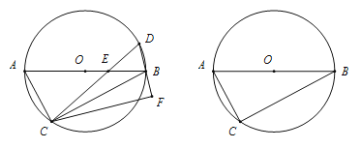
（1）如图1，当点在边上时，延长交于点，与交于点，连接．

①求证：；

②若，求的值；

（2）当正方形的边长为4，时，请直接写出的长．

Answer 1

【答案】（1）①证明见解析；②；（2）或．

【解析】

（1）通过正方形的性质和等量代换可得到，从而可用SAS证明，利用全等的性质即可得出；

（2）先证明 ，则有 ，进而可证明 ，得到，再利用得出 ，作 交EH于点P，则，利用相似三角形的性质得出，则问题可解；

（3）设，则 ，表示出EH,然后利用解出x的值，进而可求EH的长度；当E在BA的延长线上时，画出图形，用同样的方法即可求EH的长度．

（1）①证明：∵四边形ABCD，DEFG都是正方形

∴

∵

在和中，

②∵四边形DEFG是正方形

在和中，

在和中，

∵

作 交EH于点P，则

（3）当点E在AB边上时，

设，则

解得

∴

当E在BA的延长线上时，如下图

∵四边形ABCD，DEFG都是正方形

∴

∵

在和中，

∴点G在BC边上

∵四边形DEFG是正方形

在和中，

设，则

解得

∴

综上所述，EH的长度为或．