题目内容
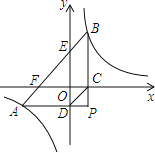
【题目】如图1所示矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 与
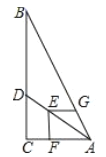
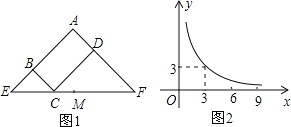
与![]() 满足的反比例函数关系如图2所示,等腰直角三角形
满足的反比例函数关系如图2所示,等腰直角三角形![]() 的斜边
的斜边![]() 过
过![]() 点,点
点,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() 为
为![]() 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )
A.当![]() 时,
时,![]()
B.当![]() 时,
时,![]()
C.当![]() 增大时,
增大时,![]() 的值增大
的值增大
D.当![]() 增大时,
增大时,![]() 的值不变
的值不变
【答案】D
【解析】
由于等腰直角三角形AEF的斜边EF过C点,则△BEC和△DCF都是直角三角形;观察反比例函数图象得反比例解析式为y=![]() ;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得CE=3
;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得CE=3![]() ,CF=3
,CF=3![]() ,则C点与M点重合;当x=9时,根据反比例函数的解析式得x=1,即BC=9,CD=1,所以EF=10
,则C点与M点重合;当x=9时,根据反比例函数的解析式得x=1,即BC=9,CD=1,所以EF=10![]() ,而EM=5
,而EM=5![]() ;利用等腰直角三角形的性质BEDF=BCCD=xy,然后再根据反比例函数的性质得BEDF=9,其值为定值;由于ECCF=
;利用等腰直角三角形的性质BEDF=BCCD=xy,然后再根据反比例函数的性质得BEDF=9,其值为定值;由于ECCF=![]() x×
x×![]() y=2xy,其值为定值.
y=2xy,其值为定值.
因为等腰直角三角形AEF的斜边EF过C点,M为EF的中点,所以△BEC和△DCF都是直角三角形;观察反比例函数图象得x=3,y=3,则反比例解析式为y=![]() .
.
A、当x=3时,y=3,即BC=CD=3,所以CE=![]() BC=3
BC=3![]() ,CF=
,CF=![]() CD=3
CD=3![]() ,C点与M点重合,则EC=EM,所以A选项错误;
,C点与M点重合,则EC=EM,所以A选项错误;
B、当x=9时,y=1,即BC=9,CD=1,所以EC=9![]() ,EF=10
,EF=10![]() ,EM=5
,EM=5![]() ,所以B选项错误;
,所以B选项错误;
C、因为ECCF=![]() x
x![]() y=2×xy=18,所以,ECCF为定值,所以选项C错误;
y=2×xy=18,所以,ECCF为定值,所以选项C错误;
D、因为BEDF=BCCD=xy=9,即BEDF的值不变,所以D选项正确.
故选:D.

【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图像与性质,研究过程如下,请补充完整.
的图像与性质,研究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
|
|
| 10 |
| -2 | 1 |
| 1 | -2 | 3 | 10 |
|
其中,![]() _______,
_______,![]() =________;
=________;
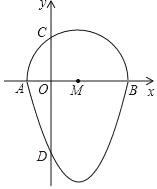
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图像;
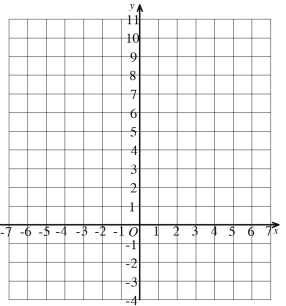
(3)观察函数图像:
①写出函数的一条图像性质:__________;
②当方程![]() 有且仅有两个不相等的实数根,根据函数图像直接写出
有且仅有两个不相等的实数根,根据函数图像直接写出![]() 的取值范围为________.
的取值范围为________.