题目内容
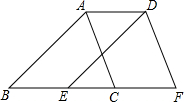 如图,点B、E、C、F在同一直线上,AB=DE,∠B=∠DEF,BE=CF.
如图,点B、E、C、F在同一直线上,AB=DE,∠B=∠DEF,BE=CF.(1)△ABC≌△DEF吗?为什么?
(2)判断四边形ACFD的形状,并说明理由.
考点:平行四边形的判定,全等三角形的判定与性质
专题:
分析:(1)根据全等三角形的判定定理SAS证得△ABC≌△DEF;
(2)利用(1)的全等三角形的对应边、对应角相等得到AC=DF,∠ACB=∠F.则由平行线的判定定理推知AC∥DF.所以由“有一组对边相等且平行的四边形是平行四边形”推知四边形ACFD是平行四边形.
(2)利用(1)的全等三角形的对应边、对应角相等得到AC=DF,∠ACB=∠F.则由平行线的判定定理推知AC∥DF.所以由“有一组对边相等且平行的四边形是平行四边形”推知四边形ACFD是平行四边形.
解答:解:(1)△ABC≌△DEF.理由如下:
∵BE=CF,
∴BE+EC=CF+EC.即BC=EF.
在△ABC与△DEF中,
∴△ABC≌△DEF(SAS);
(2)四边形ACFD是平行四边形.理由如下:
∵△ABC≌△DEF,
∴AC=DF,∠ACB=∠F.
∴AC∥DF.
∴四边形ACFD是平行四边形.
∵BE=CF,
∴BE+EC=CF+EC.即BC=EF.
在△ABC与△DEF中,
|
∴△ABC≌△DEF(SAS);
(2)四边形ACFD是平行四边形.理由如下:
∵△ABC≌△DEF,
∴AC=DF,∠ACB=∠F.
∴AC∥DF.
∴四边形ACFD是平行四边形.
点评:本题考查了全等三角形的判定与性质,平行四边形的判定与性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
 如图是由5个相同的正方体组成的一个立体图形,它的三视图是( )
如图是由5个相同的正方体组成的一个立体图形,它的三视图是( )A、 |
B、 |
C、 |
D、 |
 如图是一副三角板叠放的示意图,则∠α=
如图是一副三角板叠放的示意图,则∠α= 如图,在直角坐标系中,O是原点,已知A(4,3),P是坐标轴上的一点,若以O,A,P三点组成的三角形为等腰三角形,则满足条件的点P共有
如图,在直角坐标系中,O是原点,已知A(4,3),P是坐标轴上的一点,若以O,A,P三点组成的三角形为等腰三角形,则满足条件的点P共有 徐州市泉山区四中学生组织公益活动,有小学生、初中生、高中生和大学生参加,共1000人.各类学生人数比例见扇形统计图.
徐州市泉山区四中学生组织公益活动,有小学生、初中生、高中生和大学生参加,共1000人.各类学生人数比例见扇形统计图.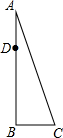 如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC滑到C处,另一只猴子从D处滑到地面B处,再由B处跑到C处,已知两猴子所经路程都是15m.
如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC滑到C处,另一只猴子从D处滑到地面B处,再由B处跑到C处,已知两猴子所经路程都是15m.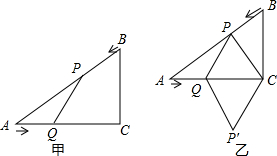 如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题: