题目内容
3.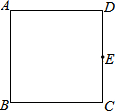 如图,在正方形ABCD中,E是边CD的中点.
如图,在正方形ABCD中,E是边CD的中点.(1)用直尺和圆规作⊙O,使⊙O经过点A、B、E(保留作图痕迹,不写作法);
(2)若正方形ABCD的边长为2,求(1)中所作⊙O的半径.
分析 (1)连接AE,分别作出AE,AB的垂直平分线,进而得到交点,即为圆心,求出答案;
(2)根据题意首先得出四边形AFE′D是矩形,进而利用勾股定理得出答案.
解答 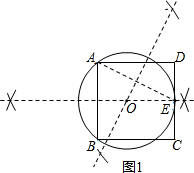 解:(1)如图1所示:
解:(1)如图1所示:
⊙O即为所求.
(2)如图2,在(1)中设AB的垂直平分线交AB于点F,交CD于点E′.
则AF=$\frac{1}{2}$AB=1,∠AFE′=90°,
∵四边形ABCD是正方形,
∴∠FAD=∠D=90°,
∴四边形AFE′D是矩形,
∴E′F=AD=2,DE′=AF=1,
∴点E′与点E重合,
连接OA,设⊙O的半径为r,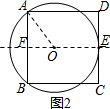
可得OA=OE=r,
∴OF=EF-OE=2-r,
∴在Rt△AOF中,AO2=AF2+OF2,
∴r2=12+(2-r)2,
∴解得:r=$\frac{5}{4}$,
∴⊙O的半径为$\frac{5}{4}$.
点评 此题主要考查了复杂作图以及勾股定理和矩形的判定与性质等知识,正确应用勾股定理是解题关键.

练习册系列答案
相关题目
14.据统计2015年1月至2016年1月,聊城市东昌湖、光岳楼、山陕会馆、宋代铁塔、古运河、姜提乐园、凤凰苑科技观光园、梦幻乐园等各景区共接待游客约518000人,这个数可用科学记数法表示为( )
| A. | 0.518×104 | B. | 5.18×105 | C. | 51.8×104 | D. | 518×103 |
11.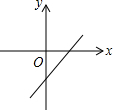 一次函数y=kx-(2-b)的图象如图所示,则k和b的取值范围是( )
一次函数y=kx-(2-b)的图象如图所示,则k和b的取值范围是( )
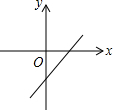 一次函数y=kx-(2-b)的图象如图所示,则k和b的取值范围是( )
一次函数y=kx-(2-b)的图象如图所示,则k和b的取值范围是( )| A. | k>0,b>2 | B. | k>0,b<2 | C. | k<0,b>2 | D. | k<0,b<2 |
8.九(1)班一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男生、女生人数之比为( )
| A. | 1:2 | B. | 2:1 | C. | 2:3 | D. | 3:2 |
13.已知,关于x的一元二次方程(m-2)x2+2x+1=0有实数根,则m的取值范围是( )
| A. | m<3 | B. | m≤3 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
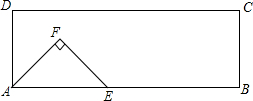 如图,在矩形ABCD中,AB=6cm,AD=2cm,点E从点A开始,沿射线AB方向平移,在平移过程中,以线段AE为斜边向上作等腰三角形AEF,当EF过点C时,点E停止移动,设点E平移的距离为x(cm),△AEF与矩形ABCD重叠部分的面积为y(cm2).
如图,在矩形ABCD中,AB=6cm,AD=2cm,点E从点A开始,沿射线AB方向平移,在平移过程中,以线段AE为斜边向上作等腰三角形AEF,当EF过点C时,点E停止移动,设点E平移的距离为x(cm),△AEF与矩形ABCD重叠部分的面积为y(cm2).