题目内容
20.如图,已知抛物线$y=\frac{1}{4}{x^2}+bx+c$交y轴于点C(0,-3),与x轴交于点A,B(点A在点B右侧),且OA=2OC
(1)求该抛物线的表达式及顶点M坐标;
(2)在线段OA上的点D,满足S△CMA=S△DMA,求D点坐标;
(3)求sin∠MCA的值.
分析 (1)已知C的坐标,则OC即可求得,根据OA=2OC即可气度而OA的长,得到A的坐标,然后把A和C的坐标代入解析式求得b和c的值,求得函数解析式,再利用配方法求得顶点坐标;
(2)根据S△CMA=S△DMA,可得CD∥AM,首先求得AM的解析式,则CD的解析式即可求得,则D的坐标即可得到;
(3)过M作AC的垂线,垂足为H,根据三角函数的定义即可求得.
解答 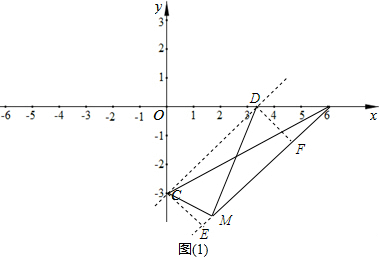 解:(1)∵抛物线$y=\frac{1}{4}{x^2}+bx+c$交y轴于点C(0,-3),与x轴交于点A,B
解:(1)∵抛物线$y=\frac{1}{4}{x^2}+bx+c$交y轴于点C(0,-3),与x轴交于点A,B
(点A在点B右侧),且OA=2OC.
∴A(6,0),
将A,C坐标代入得:c=-3,9+6b+c=0,
可得:b=-1,解析式为$y=\frac{1}{4}{x^2}-x-3$.
顶点M(2,-4);
(2)D为线段OA上一点,且S△CMA=S△DMA
过点C,D分别作AM的垂线,垂足为E,F.
∵${S_{△CMA}}=\frac{1}{2}AM×CE,{S_{△DMA}}=\frac{1}{2}AM×DF$,
∴DF=CE,又D,C在AM同侧,
∴CD∥AM,
设直线AM的解析式是y=kx+b,
则$\left\{\begin{array}{l}{6k+b=0}\\{2k+b=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-6}\end{array}\right.$,
则AM的解析式是:y=x-6,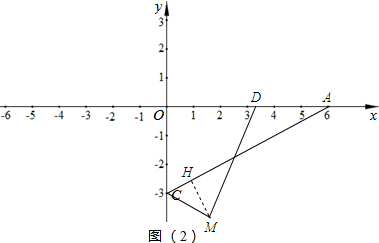
设CD的解析式是y=x+d,
把(0,-3)代入得d=-3.
则CD的解析式是:y=x-3,
令y=0,则x=3,则D的坐标是(3,0);
(3)过M作AC的垂线,垂足为H,如图(2).
由上题结论,易知S△CMA=S△DMA=6,
又AC=$3\sqrt{5}$,
则MH=$\frac{{4\sqrt{5}}}{5}$,
又CM=$\sqrt{5}$,
∴sin∠MCA=$\frac{4}{5}$.
点评 本题考查了待定系数法求函数解析式,以及三角函数的定义,正确根据S△CMA=S△DMA,得到CD∥AM是解决本题的关键.

 如图是一个正方体的展开图,在原正方体中和“国”字相对的面上的字是( )
如图是一个正方体的展开图,在原正方体中和“国”字相对的面上的字是( )| A. | 中 | B. | 钓 | C. | 鱼 | D. | 岛 |
 如图,若BO⊥OA,CO⊥0A,则0B与OC共线,其理由是过直线上一点有且只有一条直线与已知直线垂直.
如图,若BO⊥OA,CO⊥0A,则0B与OC共线,其理由是过直线上一点有且只有一条直线与已知直线垂直. 某项工程由甲、乙两个工程队合作完成,先由甲队单独做3天,剩下的工作由甲、乙两工程队合作完成,工程进度满足如图所示的函数关系:
某项工程由甲、乙两个工程队合作完成,先由甲队单独做3天,剩下的工作由甲、乙两工程队合作完成,工程进度满足如图所示的函数关系: 如图,一直动点A在函数$y=\frac{4}{x}(x>0)$的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交于x轴于点P、Q,当$\frac{QE}{DP}=\frac{4}{9}$时,图中阴影部分的面积等于$\frac{13}{3}$.
如图,一直动点A在函数$y=\frac{4}{x}(x>0)$的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交于x轴于点P、Q,当$\frac{QE}{DP}=\frac{4}{9}$时,图中阴影部分的面积等于$\frac{13}{3}$. 如图,直线y=2(x-2)+n经过原点,与双曲线$y=\frac{n}{x}$相交与点A、B,过点A作AC垂直于x轴,过点B作BC垂直于y轴,AC与BC相交于点C.求:
如图,直线y=2(x-2)+n经过原点,与双曲线$y=\frac{n}{x}$相交与点A、B,过点A作AC垂直于x轴,过点B作BC垂直于y轴,AC与BC相交于点C.求: 已知:点A、B、P为⊙O上的点,若∠PBO=15°,且PA∥OB,则∠AOB=30°.
已知:点A、B、P为⊙O上的点,若∠PBO=15°,且PA∥OB,则∠AOB=30°.