题目内容
14.在根式①$\sqrt{{x^2}+1}$②$\sqrt{\frac{x}{5}}$③$\sqrt{{x^2}-xy}$④$\sqrt{27xy}$中,最简二次根式是( )| A. | ①② | B. | ③④ | C. | ①③ | D. | ①④ |
分析 直接根据最简二次根式的定义求解.
解答 解:①$\sqrt{{x^2}+1}$不能化简,是最简二次根式;
②$\sqrt{\frac{x}{5}}$=$\frac{\sqrt{5x}}{5}$,不是最简二次根式;
③$\sqrt{{x^2}-xy}$,不能化简,是最简二次根式;
④$\sqrt{27xy}$=3$\sqrt{3xy}$,不是最简二次根式;
故选C.
点评 本题考查了最简二次根式:满足①被开方数不含分母;②被开方数中不含开得尽方的因数或因式的二次根式叫最简二次根式.

练习册系列答案
相关题目
2.某公司开发出一种高科技电子节能产品,投资2500万元一次性购买整套生产设备,此外生产每件产品需成本20元,每年还需投入500万广告费,按规定该产品的售价不得低于30元/件且不得高于70元/件,该产品的年销售量y(万件)与售价x(元/件)之间的函数关系如下表:
(1)求y与x的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?并求出当盈利最大或亏损最小时该产品的售价;
(3)在(2)的前提下,即在第一年盈利最大或亏损最小时,第二年公司重新确定产品定价,能否使两年盈利3500万元?若能,求第二年产品的售价;若不能,说明理由.
| x(元/件) | 30 | 31 | … | 70 |
| y(万件) | 120 | 119 | … | 80 |
(2)第一年公司是盈利还是亏损?并求出当盈利最大或亏损最小时该产品的售价;
(3)在(2)的前提下,即在第一年盈利最大或亏损最小时,第二年公司重新确定产品定价,能否使两年盈利3500万元?若能,求第二年产品的售价;若不能,说明理由.
4.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )
| A. | $\left\{\begin{array}{l}x+y=100\\ 3x+3y=100\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=100\\ x+\frac{1}{3}y=100\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x+y=100\\ 3x+\frac{1}{3}y=100\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=100\\ 3x+y=100\end{array}\right.$ |
 如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=2,P是△ABC所在平面内一点,且满足PA⊥PB,则PC的取值范围为$\sqrt{5}$-1≤PC≤$\sqrt{5}$+1.
如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=2,P是△ABC所在平面内一点,且满足PA⊥PB,则PC的取值范围为$\sqrt{5}$-1≤PC≤$\sqrt{5}$+1.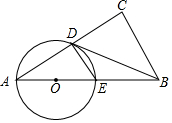 如图,在Rt△ABC中,∠C=90°,点D是AC的中点,过点A、D作⊙O,⊙O与AB交于点E,AE是⊙O的直径,AD是⊙O的一条弦,且∠A+∠CDB=90°,AD:AE=4:5,BC=6.
如图,在Rt△ABC中,∠C=90°,点D是AC的中点,过点A、D作⊙O,⊙O与AB交于点E,AE是⊙O的直径,AD是⊙O的一条弦,且∠A+∠CDB=90°,AD:AE=4:5,BC=6.