题目内容
2.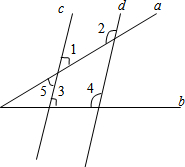 直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°.
直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°.证明:∵∠3+∠4=180°(已知)
∴c∥d (同旁内角互补,两直线平行)
∴∠1+∠2=180°(两直线平行,同旁内角互补)
∵∠1=∠5(对顶角相等)
∴∠2+∠5=180°等量代换.
分析 由同旁内角互补得出c∥d,得出同旁内角互补∠1+∠2=180°,再由对顶角相等即可得出结论.
解答 证明:∵∠3+∠4=180°(已知)
∴c∥d (同旁内角互补,两直线平行 )
∴∠1+∠2=180°(两直线平行,同旁内角互补)
∵∠1=∠5( 对顶角相等)
∴∠2+∠5=180°(等量代换).
故答案为:同旁内角互补,两直线平行;∠1+∠2=180°;∠5;对顶角相等;等量代换.
点评 本题考查了平行线的判定与性质、对顶角相等的性质;熟练掌握平行线的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
7. 如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )
如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )
 如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )
如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 16cm |
11. 如图,点O到直线AB的距离是指哪条线段的长?( )
如图,点O到直线AB的距离是指哪条线段的长?( )
 如图,点O到直线AB的距离是指哪条线段的长?( )
如图,点O到直线AB的距离是指哪条线段的长?( )| A. | OA | B. | AB | C. | OC | D. | BC |
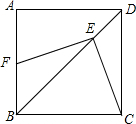 如图,在正方形ABCD中,E是对角线BD上一点,过点E作EF⊥CE,交AB于点F,BF=2,BC=6,则EF=2$\sqrt{5}$.
如图,在正方形ABCD中,E是对角线BD上一点,过点E作EF⊥CE,交AB于点F,BF=2,BC=6,则EF=2$\sqrt{5}$. 已知:抛物线C1:y=x2-2x-3.
已知:抛物线C1:y=x2-2x-3.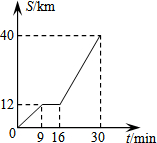 如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题: 如图是一个4×4的正方形网格,图中所标示的7个角的角度之和等于585°.
如图是一个4×4的正方形网格,图中所标示的7个角的角度之和等于585°.