题目内容
20.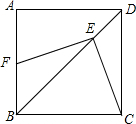 如图,在正方形ABCD中,E是对角线BD上一点,过点E作EF⊥CE,交AB于点F,BF=2,BC=6,则EF=2$\sqrt{5}$.
如图,在正方形ABCD中,E是对角线BD上一点,过点E作EF⊥CE,交AB于点F,BF=2,BC=6,则EF=2$\sqrt{5}$.
分析 连接CF,由正方形的性质得出∠B=90°,∠DBC=45°,再由EF⊥CE,证得B、C、E、F四点共圆,得出△CEF为等腰直角三角形,求得EF=$\frac{CF}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$CF,再由勾股定理求得CF即可.
解答 解:连接CF,如图所示:
∵四边形ABCD为正方形,
∴∠B=90°,∠DBC=45°,
∵EF⊥CE,
∴∠CEF=90°,
∴B、C、E、F四点共圆,
∴∠EFC=∠DBC=45°,
∴△CEF为等腰直角三角形,
∴EF=$\frac{CF}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$CF,
由勾股定理得:CF=$\sqrt{B{C}^{2}+B{F}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
∴EF=$\frac{\sqrt{2}}{2}$×2$\sqrt{10}$=2$\sqrt{5}$,
故答案为:2$\sqrt{5}$.
点评 本题考查了正方形1性质、勾股定理、四点共圆、圆周角定理、等腰直角三角形的判定与性质;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
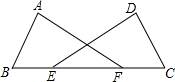 已知:BE=CF,AB=CD,∠B=∠C.求证:AF=DE.
已知:BE=CF,AB=CD,∠B=∠C.求证:AF=DE. 如图,△ABC中,BC=a.
如图,△ABC中,BC=a. 如图所示的几何体是由16个棱长为1厘米的小正方体堆积而成的,问这个几何体的表面积是多少平方厘米?
如图所示的几何体是由16个棱长为1厘米的小正方体堆积而成的,问这个几何体的表面积是多少平方厘米?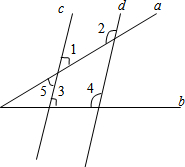 直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°.
直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°.