题目内容
9.化简求值:已知a=2+$\sqrt{2}$,b=2-$\sqrt{2}$,求代数式(a-b+$\frac{4ab}{a-b}$)•(a+b-$\frac{4ab}{a+b}$)的值.分析 原式括号中通分并利用同分母分式的加减法则计算,约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:原式=$\frac{(a-b)^{2}+4ab}{a-b}$•$\frac{(a+b)^{2}-4ab}{a+b}$=$\frac{(a+b)^{2}}{a-b}$•$\frac{(a-b)^{2}}{a+b}$=(a+b)(a-b),
当a=2+$\sqrt{2}$,b=2-$\sqrt{2}$时,原式=8$\sqrt{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.下列图形中,轴对称图形的个数为( )

| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
20.下列长度的三条线段能构成三角形的是( )
| A. | 3,4,8 | B. | 3,4,7 | C. | 5,6,10 | D. | 5,6,11 |
17.某学校组织知识竞赛,共设有20道试题,其中有关中国优秀传统文化试题10道,实践应用试题6道,创新能力试题4道.小捷从中任选一道试题作答,他选中创新能力试题的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
14. 如图,A、B、C为⊙O上的任意三点,若∠BOC=100°,则∠BAC的度数为( )
如图,A、B、C为⊙O上的任意三点,若∠BOC=100°,则∠BAC的度数为( )
 如图,A、B、C为⊙O上的任意三点,若∠BOC=100°,则∠BAC的度数为( )
如图,A、B、C为⊙O上的任意三点,若∠BOC=100°,则∠BAC的度数为( )| A. | 50° | B. | 80° | C. | 100° | D. | 130° |
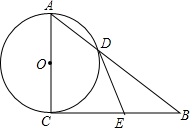 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E. 章丘市积极推进新农村建设,在城区与每个乡镇之间都开通了每半小时一班的公 交车,如图,是通往某镇的甲、乙两辆公交车分别从客运中心和某镇两地出发相向而行的时间和距离客运中心的关系图,图中l1、l2表示两辆公交车与客运中心的距离S (千米)与行驶时间t(小时)之间的关系,则下列说法:
章丘市积极推进新农村建设,在城区与每个乡镇之间都开通了每半小时一班的公 交车,如图,是通往某镇的甲、乙两辆公交车分别从客运中心和某镇两地出发相向而行的时间和距离客运中心的关系图,图中l1、l2表示两辆公交车与客运中心的距离S (千米)与行驶时间t(小时)之间的关系,则下列说法: