题目内容
已知a,b,c是三角形三边长,且b2-2bc+c2=ac-ab,试判断三角形形状.
考点:因式分解的应用
专题:
分析:由b2-2bc+c2=ac-ab变形,利用因式分解可得到(b-c)(b-c-a)=0,结合三角形的三边关系可得出b=c,可判断出其形状.
解答:解:∵b2-2bc+c2=ac-ab,
∴b2-2bc+c2-a(b-c)=0,
∴(b-c)(b-c-a)=0,
∵b-c<a,
∴b-c=0,
∴b=c,
∴三角形为等腰三角形.
∴b2-2bc+c2-a(b-c)=0,
∴(b-c)(b-c-a)=0,
∵b-c<a,
∴b-c=0,
∴b=c,
∴三角形为等腰三角形.
点评:本题主要考查因式分解的应用,由等式得到(b-c)(b-c-a)=0是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
下列说法中错误的是( )
| A、一组对边平行且一组对角相等的四边形是平行四边形 |
| B、四个角都相等的四边形是矩形 |
| C、每组邻边都相等的四边形是菱形 |
| D、对角线互相垂直的平行四边形是正方形 |
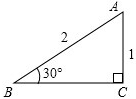 要求tan30°的值,可构造如图所示的直角三角形进行计算,作Rt△ABC,使∠C=90°,斜边AB=2,直角边AC=1,那么BC=
要求tan30°的值,可构造如图所示的直角三角形进行计算,作Rt△ABC,使∠C=90°,斜边AB=2,直角边AC=1,那么BC=