题目内容
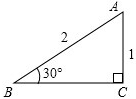要求tan30°的值，可构造如图所示的直角三角形进行计算，作Rt△ABC，使∠C=90°，斜边AB=2，直角边AC=1，那么BC=| 3 |
| AC |
| BC |
| 1 | ||
|
| ||
| 3 |
考点：解直角三角形
专题：阅读型
分析：根据角平分线的性质以及勾股定理首先求出CD的长，进而得出tan15°=
，tan75°=
求出即可．
| CD |
| BC |
| BC |
| CD |
解答：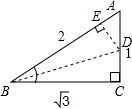
解：作∠B的平分线交AC于点D，作DE⊥AB，垂足为E，
∵BD平分∠ABC，CD⊥BC，DE⊥AB，
∴CD=DE，
设CD=x，则AD=1-x，AE=2-BC=2-BE=2-
，
在Rt△ADE中，
CD2+AE2=AD2
x2+（2-
）2=（1-x）2，
解得：x=2
-3，
∴tan15°=
=
=2-
，tan75°=
=
=2+
．
解：作∠B的平分线交AC于点D，作DE⊥AB，垂足为E，∵BD平分∠ABC，CD⊥BC，DE⊥AB，
∴CD=DE，
设CD=x，则AD=1-x，AE=2-BC=2-BE=2-
| 3 |
在Rt△ADE中，
CD2+AE2=AD2
x2+（2-
| 3 |
解得：x=2
| 3 |
∴tan15°=
| CD |
| BC |
2
| ||
|
| 3 |
| BC |
| CD |
| ||
2
|
| 3 |
点评：此题主要考查了解直角三角形和勾股定理等知识，根据已知得出CD的长是解题关键．
练习册系列答案
相关题目
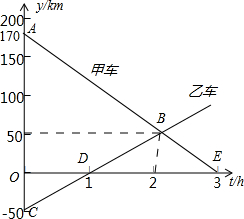甲、乙两辆汽车在同一条公路上同时匀速行驶，图中的两条线分别表示甲、乙两车距M站的距离y（km）与它们行驶的时间t（h）之间的函数关系式，请根据图象回答下列问题．
如图是由几个棱长为1cm的小立方块搭成的几何体从上往下看的平面图形，小立方块中的数字表示该位置上小立方块的个数，求出这个几何体的体积．