题目内容
14.四边形的四边顺次为a、b、c、d,且满足a2+b2+c2+d2=2(ab+cd),则这个四边形一定是( )| A. | 对角线互相垂直的四边形 | B. | 两组对角分别相等的四边形 | ||
| C. | 平行四边形 | D. | 对角线长相等的四边形 |
分析 首先把a2+b2+c2+d2=2(ab+cd)变形为a2+b2+c2+d2-2ab-2cd=0,然后利用完全平方公式分解因式和非负数的性质即可求解.
解答  解:∵a2+b2+c2+d2=2(ab+cd),
解:∵a2+b2+c2+d2=2(ab+cd),
∴a2+b2+c2+d2-2ab-2cd=0,
∴(a-b)2+(c-d)2=0,
∴a-b=0且c-d=0,
∴a=b且c=d.
如图,点A在BD的垂直平分线上,点C在BD的垂直平分线上,
∴AC垂直平分线BD,
∴四边形ABCD是对角线互相垂直的四边形.
故选A.
点评 此题主要考查了因式分解的应用,解题时首先利用因式分解把等式变形,然后利用非负数的性质即可解决问题.

练习册系列答案
相关题目
5.下列说法正确的是( )
| A. | 0没有平方根 | B. | -1的平方根是-1 | ||
| C. | 4的算术平方根是2 | D. | (-3)2的平方根是3 |
2.下列性质中,矩形具有但平行四边形不一定具有的是( )
| A. | 对边相等 | B. | 对角相等 | C. | 对角线相等 | D. | 对角线互相平分 |
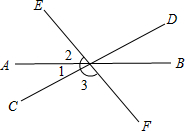 已知:如图,∠2=2∠1,∠3=3∠2,求∠DOE的度数.
已知:如图,∠2=2∠1,∠3=3∠2,求∠DOE的度数. 如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接AF交对角线于点E,连接EC
如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接AF交对角线于点E,连接EC