题目内容
15.Rt△ABC中,∠C=90°,∠A=45°,AB=$\sqrt{2}$,则AC=1.分析 根据三角形内角和公式可得∠B=45°,根据等角对等边可得AC=BC,再利用勾股定理计算出AC长即可.
解答 解:∵∠C=90°,∠A=45°,
∴∠B=45°,
∴AC=BC,
设AC=BC=x,
∵AC2+BC2=AB2,
∴x2+x2=($\sqrt{2}$)2,
解得:x=1或-1(舍去),
∴AC=1,
故答案为:1.
点评 此题主要考查了勾股定理,关键是掌握直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
13.在现实生活中,铺地最常见的是用正方形地板砖,某小区广场准备用多种地板砖组合铺设,则能够选择的组合是( )
| A. | 正三角形,正方形 | B. | 正方形,正六边形 | ||
| C. | 正五边形,正六边形 | D. | 正六边形,正八边形 |
6.某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为x(0<x<0.5).
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
| 项目 | 第一次锻炼 | 第二次锻炼 |
| 步数(步) | 10000 | ①10000(1+3x) |
| 平均步长(米/步) | 0.6 | ②0.6(1-x) |
| 距离(米) | 6000 | 7020 |
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
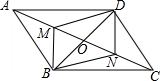 如图,在平行四边形ABCD中,M、N分别是OA,OC的中点,O为对角线AC与BD的交点,试问四边形BMDN是平行四边形吗?说说你的理由.
如图,在平行四边形ABCD中,M、N分别是OA,OC的中点,O为对角线AC与BD的交点,试问四边形BMDN是平行四边形吗?说说你的理由. 如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24cm,△OAB的周长是18cm,则EF=3cm.
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24cm,△OAB的周长是18cm,则EF=3cm.
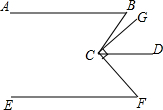 如图,已知AB∥CD,GC⊥CF,∠ABC=65°,CD是∠GCF的角平分线,∠EFC=40°.
如图,已知AB∥CD,GC⊥CF,∠ABC=65°,CD是∠GCF的角平分线,∠EFC=40°.