题目内容
17.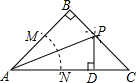 如图,在等腰直角△ABC中,B=90°,以点A为圆心任意长为半径画弧,与AB,AC分别交于点M,N,分别以点M,N为圆心大于$\frac{1}{2}$MN长为半径画弧,两弧交于点P,且点P刚好落在边BC上,AB=10cm,下列说法中:
如图,在等腰直角△ABC中,B=90°,以点A为圆心任意长为半径画弧,与AB,AC分别交于点M,N,分别以点M,N为圆心大于$\frac{1}{2}$MN长为半径画弧,两弧交于点P,且点P刚好落在边BC上,AB=10cm,下列说法中:①AB=AD;②AP平分∠BAC;③△PDC的周长是10$\sqrt{2}$cm;④AN=ND,
正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 根据角平分线做法得出AP平分∠BAC,进而结合全等三角形的判定与性质以及结合等腰直角三角形的性质分别判断得出答案.
解答 解:由题意可得:AP平分∠BAC,则
在△ABP和△ADP中
∵$\left\{\begin{array}{l}{∠B=∠ADP}\\{∠BAP=∠PAD}\\{AP=AP}\end{array}\right.$,
∴△ABP≌△ADP(AAS),
∴AB=AD,故①正确;
由角平分线的做法可得②AP平分∠BAC,故此选项正确;
∵等腰直角△ABC,
∴∠C=45°,则△PDC是等腰直角三角形,
∴DP=DC=DP,
∴③△PDC的周长是:PD+DC+PC=BP+PC+DC=BC+DC=AB+DC=AD+DC=AC=10$\sqrt{2}$cm,故此选项正确.
故选:A.
点评 此题主要考查了角平分线的作法以及等腰直角三角形的性质和全等三角形的判定与性质等知识,根据角平分线的作法得出AP是∠BAC的平分线是解题的关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
6. 如图,点P为等边△ABC的边AB上一点,点Q为BC延长线上一点,PA=CQ,连接PQ交AC于D,若CD=3,BQ=10,则PA的长为( )
如图,点P为等边△ABC的边AB上一点,点Q为BC延长线上一点,PA=CQ,连接PQ交AC于D,若CD=3,BQ=10,则PA的长为( )
 如图,点P为等边△ABC的边AB上一点,点Q为BC延长线上一点,PA=CQ,连接PQ交AC于D,若CD=3,BQ=10,则PA的长为( )
如图,点P为等边△ABC的边AB上一点,点Q为BC延长线上一点,PA=CQ,连接PQ交AC于D,若CD=3,BQ=10,则PA的长为( )| A. | 2 | B. | 2.2 | C. | 2.5 | D. | 2.4 |
12.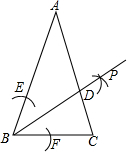 如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于$\frac{1}{2}$EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于$\frac{1}{2}$EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
 如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于$\frac{1}{2}$EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于$\frac{1}{2}$EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.| A. | 65 | B. | 75 | C. | 80 | D. | 85 |
6.计算(-3)×9的值是( )
| A. | 6 | B. | 27 | C. | -12 | D. | -27 |
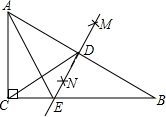 如图,在△ABC中,∠ACB=90°,分别以点A、点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD、AE,请你依作图信息写一个正确的结论AE=BE(答案不唯一).
如图,在△ABC中,∠ACB=90°,分别以点A、点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD、AE,请你依作图信息写一个正确的结论AE=BE(答案不唯一).
 如图所示,在等腰三角形ABC中,AB=AC,若BC=$\sqrt{3}$AB,求∠B的三个三角函数值.
如图所示,在等腰三角形ABC中,AB=AC,若BC=$\sqrt{3}$AB,求∠B的三个三角函数值. 如图,在Rt△ABC中,∠ABC=60°,$BC=\sqrt{3}$.
如图,在Rt△ABC中,∠ABC=60°,$BC=\sqrt{3}$. 如图,正方形ABCD边长是4,P是CD中点,Q是线段BC上一点,当CQ=4或1时,以由Q,C,P三点为顶点的三角形与△ADP相似.
如图,正方形ABCD边长是4,P是CD中点,Q是线段BC上一点,当CQ=4或1时,以由Q,C,P三点为顶点的三角形与△ADP相似.