题目内容
13. 在△ABC中,点D为BC上一点,连接AD,点E在BD上,且DE=CD,过点E作AB的平行线交AD于F,且EF=AC.如图,求证:∠BAD=∠CAD.
在△ABC中,点D为BC上一点,连接AD,点E在BD上,且DE=CD,过点E作AB的平行线交AD于F,且EF=AC.如图,求证:∠BAD=∠CAD.
分析 延长FD到点G,过C作CG∥AB交FD的延长线于点M,可证明△EDF≌△CMD,可得CM=EF=AC,进一步得到结论;
解答 证明: 延长FD到点G,过C作CG∥AB交FD的延长线于点M,
延长FD到点G,过C作CG∥AB交FD的延长线于点M,
则EF∥MC,
∴∠BAD=∠EFD=∠M,
在△EDF和△CMD中,$\left\{\begin{array}{l}{∠EFD=∠M}&{\;}\\{∠EDF=∠MDC}&{\;}\\{ED=DC}&{\;}\end{array}\right.$,
∴△EDF≌△CMD(AAS),
∴MC=EF=AC,
∴∠M=∠CAD,
∴∠BAD=∠CAD.
点评 本题考查了全等三角形的判定于性质、平行线的性质、等腰三角形的性质;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
 如图,四点A、B、C、D,按照下列语句画出图形;
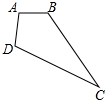
如图,四点A、B、C、D,按照下列语句画出图形; 如图,在△ABC中,∠C=90°,DE垂直平分AB,E是垂足,交BC于D,DG⊥AD于D,且DG=BD,AC=8,CD=6,求△BDG的面积.
如图,在△ABC中,∠C=90°,DE垂直平分AB,E是垂足,交BC于D,DG⊥AD于D,且DG=BD,AC=8,CD=6,求△BDG的面积.
 如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形. 已知某函数的图象如图所示,求这个函数的解析式.
已知某函数的图象如图所示,求这个函数的解析式. 已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B+∠ADE=180°.求证:BC=DE.
已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B+∠ADE=180°.求证:BC=DE.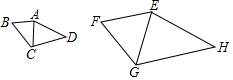 如图,四边形ABCD∽四边形EFGH,连接相应的对角线AC,EG.
如图,四边形ABCD∽四边形EFGH,连接相应的对角线AC,EG.