题目内容
14．
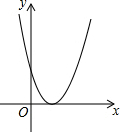已知二次函数y=ax2+bx+c的图象如图所示，则a＞0，b＜0，c＞0，△=0．（用“＜”，“=”或“＞”号连接）
分析 根据抛物线的开口方向，对称轴位置，与y轴交点的位置，与x轴交点的个数即可判断．
解答 解：由开口方向可知：a＞0，
由对称轴可知：-$\frac{b}{2a}$＞0，
∴b＜0，
∵抛物线与y轴交点在y的正半轴，
∴c＞0，
∵抛物线与x轴只有一个交点，
∴△=0，
故答案为：a＞0，b＜0，c＜0，△=0．
点评 本题考查二次函数的图象与性质，只要根据图象的位置，即可判断a、b、c和△与0的大小关系．
练习册系列答案
字词句段篇系列答案
相关题目
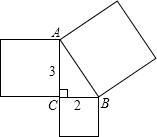如图，直角三角形ABC的两条直角边AC=3，BC=2，分别以Rt△ABC的三边为边向外作正方形．
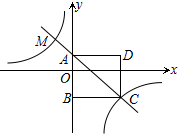如图，四边形ABCD为正方形，点A的坐标为（0，1），点B的坐标为（0，-2），反比例函数y=$\frac{k}{x}$的图象经过点C，一次函数y=ax+b的图象经过A、C两点．