题目内容
3.(1)如果等腰三角形的周长为14,底边长为6,那么腰长为4;(2)如果等腰三角形的周长为14,腰长为6,那么底边长为2;
(3)如果等腰三角形的周长为10,一边长为4,那么另两边长分别为4,2或3,3.
分析 (1)由等腰三角形的周长为14,底边长为6,根据等腰三角形的两腰相等,即可求得其腰长的值;
(2)由等腰三角形的周长为14,腰长为6,根据等腰三角形的两腰相等,即可求得其底边长的值;
(3)题目给出等腰三角形一条边长为3,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形..
解答 解:(1)(14-6)÷2
=8÷2
=4.
故腰长为4.
(2)14-6×2
=14-12
=2.
故底边长为2.
(3)①当4是腰长时,底边为10-4×2=2,
此时4、4、2三边能够组成三角形,
所以另两边长为4,2;
②当4为底边长时,腰长为$\frac{1}{2}$×(10-4)=3,
此时3、3、4能够组成三角形,
所以另两边长为3,3.
所以另两边的长分别是4,2或3,3.
故答案为:4;2;4,2或3,3.
点评 本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.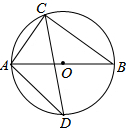 如图,已知AB是⊙O的直径,C点在⊙O上,CD平分∠ACB,若AC=6,BC=8,则AD长为( )
如图,已知AB是⊙O的直径,C点在⊙O上,CD平分∠ACB,若AC=6,BC=8,则AD长为( )
 如图,已知AB是⊙O的直径,C点在⊙O上,CD平分∠ACB,若AC=6,BC=8,则AD长为( )
如图,已知AB是⊙O的直径,C点在⊙O上,CD平分∠ACB,若AC=6,BC=8,则AD长为( )| A. | $\frac{4}{3}$ | B. | 5 | C. | 5$\sqrt{3}$ | D. | 5$\sqrt{2}$ |
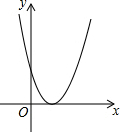 已知二次函数y=ax2+bx+c的图象如图所示,则a>0,b<0,c>0,△=0.(用“<”,“=”或“>”号连接)
已知二次函数y=ax2+bx+c的图象如图所示,则a>0,b<0,c>0,△=0.(用“<”,“=”或“>”号连接) 如图,△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D,E,BE=4CE,AD=$\sqrt{10}$.
如图,△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D,E,BE=4CE,AD=$\sqrt{10}$.