题目内容
4.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.(1)在△ABC内放入正方形纸片DEFG,使边EF在斜边AB上,点D、G分别在AC、BC上.则正方形的边长为$\frac{120}{37}$;
(2)类似第(1)小题,使正方形纸片一条边都在AB上,若在△ABC内并排(不重叠)放入两个小正方形,且只能放入两个,试确定小正方形边长的范围;
(3)在△ABC内并排放入(不重叠)边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放16个小正方形纸片.

分析 (1)作CH⊥AB于H,交DG于P,根据勾股定理求出AB,根据三角形的面积公式求出CH,根据相似三角形的性质计算即可;
(2)根据相似三角形的性质求出两个正方形的顶点分别在AC、BC上时,x的值即可;
(3)根据题意、结合图形,根据相似三角形的性质分别计算即可.
解答 解:(1)作CH⊥AB于H,交DG于P,
∵∠C=90°,AC=6,BC=8,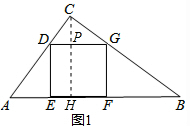
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∴CH=$\frac{\frac{1}{2}AC×BC}{\frac{1}{2}×AB}$=4.8,
∵四边形DEFG是正方形,
∴DG∥AB,
∴$\frac{DG}{AB}$=$\frac{CP}{CH}$,即$\frac{DG}{10}$=$\frac{4.8-DG}{4.8}$,
解得,DG=$\frac{120}{37}$,
故答案为:$\frac{120}{37}$;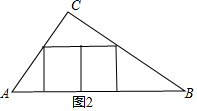
(2)如图2,当两个正方形的顶点分别在AC、BC上时,
设正方形的边长为x,
由(1)得,$\frac{2x}{10}$=$\frac{4.8-x}{4.8}$,
解得,x=$\frac{120}{49}$,
则小正方形边长x的范围是x≤$\frac{120}{49}$;
(3)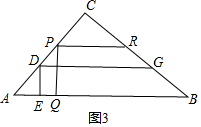 如图3,当DE=1时,
如图3,当DE=1时,
由(1)得,$\frac{DG}{10}$=$\frac{4.8-1}{4.8}$,
解得,DG=$\frac{95}{12}$,
则一条边都在AB上正方形的个数是7,
当PQ=2时,$\frac{PR}{10}$=$\frac{4.8-2}{4.8}$,
解得,PR=$\frac{35}{6}$,
则第二层正方形的个数是5,
同理,第三层正方形的个数是3,第④层正方形的个数是1,
则最多能摆放7+5+3+1=16个小正方形纸片.
故答案为:16.
点评 本题考查了正方形的性质和相似三角形的判定和性质,解题的关键是需要对正方形的性质、直角三角形的勾股定理和相似三角形的判定和性质熟练地掌握.

| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
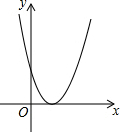 已知二次函数y=ax2+bx+c的图象如图所示,则a>0,b<0,c>0,△=0.(用“<”,“=”或“>”号连接)
已知二次函数y=ax2+bx+c的图象如图所示,则a>0,b<0,c>0,△=0.(用“<”,“=”或“>”号连接) 如图所示的是某个几何体从三种不同方向所看到的图形.
如图所示的是某个几何体从三种不同方向所看到的图形.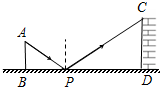 如图,是小李设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.1米,BP=1.9米,PD=19米,那么该古城墙CD的高度是11米.
如图,是小李设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.1米,BP=1.9米,PD=19米,那么该古城墙CD的高度是11米. 如图,△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D,E,BE=4CE,AD=$\sqrt{10}$.
如图,△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D,E,BE=4CE,AD=$\sqrt{10}$.