题目内容
6.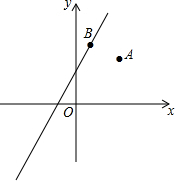 如图:点A的坐标为(3,4),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$.
如图:点A的坐标为(3,4),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$.
分析 当AB与直线y=2x+4垂直时,AB最短.求出AB的解析式,与y=2x+4组成方程组,求出其交点坐标,然后根据勾股定理求得即可.
解答 解:设AB解析式为y=kx+b(k≠0),
∵AB与直线y=2x+4垂直,
∴k=-$\frac{1}{2}$,
∴直线AB解析式为y=-$\frac{1}{2}$x+b.
将A(3,4)代入y=-$\frac{1}{2}$x+b,得
4=-$\frac{3}{2}$+b,
解得,b=$\frac{11}{2}$.
则直线AB的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$.则
$\left\{\begin{array}{l}{y=2x+4}\\{y=-\frac{1}{2}x+\frac{11}{2}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=\frac{3}{5}}\\{y=\frac{26}{5}}\end{array}\right.$.
故B点坐标为($\frac{3}{5}$,$\frac{26}{5}$).
∴AB=$\sqrt{(3-\frac{3}{5})^{2}+(4-\frac{26}{5})^{2}}$=$\frac{6}{5}$$\sqrt{5}$.
故答案是:$\frac{6}{5}$$\sqrt{5}$.
点评 本题考查了一次函数的性质和垂线段最短,找到B点是解题的关键.

练习册系列答案
相关题目
16.四边形的四条边依次为a,b,c,d且满足a2+b2+c2+d2-4(a+c)-6(b+d)+26=0.那么这个四边形的形状是( )
| A. | 一般四边形 | B. | 平行四边形 | C. | 正方形 | D. | 长方形 |
14. 如图,A,B是双曲线$y=\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,若△ADO的面积为2,D为OB的中点,则k的值为( )
如图,A,B是双曲线$y=\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,若△ADO的面积为2,D为OB的中点,则k的值为( )
 如图,A,B是双曲线$y=\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,若△ADO的面积为2,D为OB的中点,则k的值为( )
如图,A,B是双曲线$y=\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,若△ADO的面积为2,D为OB的中点,则k的值为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 6 | D. | 8 |
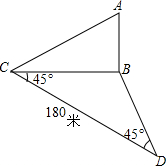 为了求河对岸建筑物AB的高,在地平面上测得基线CD=180米,在C点测得A点的仰角为30°,在地平面上测得∠BCD=∠BDC=45°,那么AB的高是30$\sqrt{6}$米.
为了求河对岸建筑物AB的高,在地平面上测得基线CD=180米,在C点测得A点的仰角为30°,在地平面上测得∠BCD=∠BDC=45°,那么AB的高是30$\sqrt{6}$米. 如图,在△ABC中,AB=AC,将△ABC沿DE折叠,使点A与点C重合,如果∠DCB=42°,求∠A的度数.
如图,在△ABC中,AB=AC,将△ABC沿DE折叠,使点A与点C重合,如果∠DCB=42°,求∠A的度数.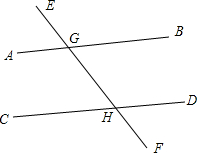 如图,判断并说明理由.
如图,判断并说明理由.