题目内容
11. 如图,在△ABC中,AB=AC,将△ABC沿DE折叠,使点A与点C重合,如果∠DCB=42°,求∠A的度数.
如图,在△ABC中,AB=AC,将△ABC沿DE折叠,使点A与点C重合,如果∠DCB=42°,求∠A的度数.
分析 设∠A=x,由翻折的性质可知∠ECD=x,则∠ACB=x+42°,由等腰三角形的性质可知∠ABC=∠ACB=x+42°,最后在△ABC中根据三角形的内角和定理列方程求解即可.
解答 解:设∠A=x,由翻折的性质可知∠ECD=x,则∠ACB=x+42°.
∵AB=AC,
∴∠ABC=∠ACB=x+42°.
在△ABC中,由三角形的内角和定理可知:x+x+42°+x+42°=180°.
解得:x=32°.
∴∠A=32°.
点评 本题主要考查的是翻折的性质、等腰三角形的性质、三角形的内角和定理,根据题意列出关于x的方程是解题的关键.

练习册系列答案
相关题目
 ;
; .
. 如图,AC∥BD,∠B=∠C,请你说明∠E=∠F的理由.
如图,AC∥BD,∠B=∠C,请你说明∠E=∠F的理由.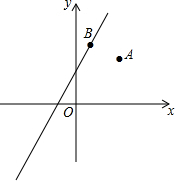 如图:点A的坐标为(3,4),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$.
如图:点A的坐标为(3,4),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$. 如图,已知直线a,b,c被直线d所截,若∠1=∠2,∠2+∠3=180°,a与c平行吗?试说明理由.
如图,已知直线a,b,c被直线d所截,若∠1=∠2,∠2+∠3=180°,a与c平行吗?试说明理由. 如图所示,直径AB垂直于弦CD,垂足为点E,如果AB=10,$\widehat{BC}$=$\frac{15}{8}$π,则$\widehat{AD}$=$\frac{25}{8}$π.
如图所示,直径AB垂直于弦CD,垂足为点E,如果AB=10,$\widehat{BC}$=$\frac{15}{8}$π,则$\widehat{AD}$=$\frac{25}{8}$π.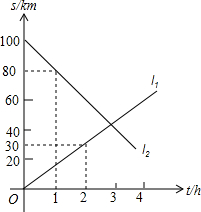 如图,l1、l2分别是甲、乙二人运动的路程与时间关系图.根据图中信息,完成下列问题:
如图,l1、l2分别是甲、乙二人运动的路程与时间关系图.根据图中信息,完成下列问题: