题目内容
11.下列各式中,是最简二次根式的是( )| A. | $\sqrt{8}$ | B. | $\sqrt{30}$ | C. | $\sqrt{\frac{1}{5}}$ | D. | $\frac{1}{{\sqrt{x}}}$ |
分析 判断一个二次根式是否为最简二次根式主要方法是根据最简二次根式的定义进行,或直观地观察被开方数的每一个因数(或因式)的指数都小于根指数2,且被开方数中不含有分母,被开方数是多项式时要先因式分解后再观察.
解答 解:A.$\sqrt{8}$=$\sqrt{{2}^{2}×2}$被开方数中含有能开的尽方的因数,所以它不是最简二次根式.故本选项错误;
B.$\sqrt{30}$符合最简二次根式的定义,所以它是最简二次根式.故本选项正确;
C.$\sqrt{\frac{1}{5}}$被开方数中含有字母,所以它不是最简二次根式.故本选项错误;
D.$\frac{1}{\sqrt{x}}$=$\frac{\sqrt{x}}{x}$被开方数中含有字母,所以它不是最简二次根式.故本选项错误;
故选B.
点评 本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或因式.

练习册系列答案
相关题目
19.化简$\frac{1}{3-2\sqrt{2}}$结果正确的是( )
| A. | 3$+2\sqrt{2}$ | B. | 3$-\sqrt{2}$ | C. | 17$+12\sqrt{2}$ | D. | 17-12$\sqrt{2}$ |
1.△ABC的三边长分别是1、k、3,则化简$7-\sqrt{4{k^2}-36k+81}-|{2k-3}|$的结果为( )
| A. | -5 | B. | 19-4k | C. | 13 | D. | 1 |
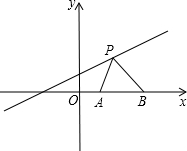 已知如图,点A(1,0),点B(2,0),点P是直线y=$\frac{1}{2}$x+1上的一个动点,PA2+PB2的最小值=$\frac{27}{5}$.
已知如图,点A(1,0),点B(2,0),点P是直线y=$\frac{1}{2}$x+1上的一个动点,PA2+PB2的最小值=$\frac{27}{5}$.
 已知:在△ABC中,∠B=45°,∠C=30°,AC=2.求:
已知:在△ABC中,∠B=45°,∠C=30°,AC=2.求: 如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOD=20°,求∠COE的度数.
如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOD=20°,求∠COE的度数.