题目内容
在△ABD和△ACE中,AD=AB,AC=AE.
(1)如图1,若∠DAB=∠CAE=60°,求证:BE=DC;
(2)如图2,若∠DAB=∠CAE=30°,求∠DOB的度数.
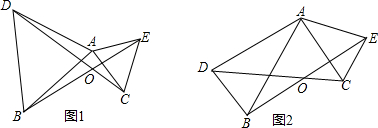
(1)如图1,若∠DAB=∠CAE=60°,求证:BE=DC;
(2)如图2,若∠DAB=∠CAE=30°,求∠DOB的度数.

考点:全等三角形的判定与性质
专题:
分析:(1)通过证明△ADC≌△ABE,利用全等三角形的性质即可得到DC=BE;
(2)同理可证明△ADC≌△ABE,利用三角形的内角和定理和三角形的外角之间的关系即可求出∠DOB的度数.
(2)同理可证明△ADC≌△ABE,利用三角形的内角和定理和三角形的外角之间的关系即可求出∠DOB的度数.
解答:解:(1)证明:∵∠DAB=∠CAE,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴BE=DC;
(2)同理得:△ADC≌△ABE,
∴∠ADC=∠ABE,
又∵∠DOB=180°-∠ODB-∠OBD=180°-∠ODB-∠ABD-∠ABE,
∴∠DOB=180°-∠ODB-∠ABD-∠ADC,=180°-∠ADB-∠ABD,
∴∠DOB=∠DAB=30°.
∴∠DAC=∠BAE,
在△DAC和△BAE中,
|
∴△DAC≌△BAE(SAS),
∴BE=DC;
(2)同理得:△ADC≌△ABE,
∴∠ADC=∠ABE,
又∵∠DOB=180°-∠ODB-∠OBD=180°-∠ODB-∠ABD-∠ABE,
∴∠DOB=180°-∠ODB-∠ABD-∠ADC,=180°-∠ADB-∠ABD,
∴∠DOB=∠DAB=30°.
点评:本题考查了全等三角形的判定和性质以及三角形的内角和定理、三角形的外角之间的数量关系,题目的综合性很强,难度中等.

练习册系列答案
相关题目
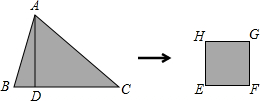 如图,张老师用一张锐角三角形纸板ABC剪出了正方形EFGH,边EF从原BC边上剪下,点H和点G分别在原AB,AC边上,已知BC=18cm,高AD=12cm,则这个正方形纸板的边长是( )
如图,张老师用一张锐角三角形纸板ABC剪出了正方形EFGH,边EF从原BC边上剪下,点H和点G分别在原AB,AC边上,已知BC=18cm,高AD=12cm,则这个正方形纸板的边长是( )| A、6cm | B、6.8cm |
| C、7.2cm | D、9cm |
 如图,梯子的各条横档互相平行,如果∠1=110°,则∠2的度数为( )
如图,梯子的各条横档互相平行,如果∠1=110°,则∠2的度数为( )| A、60° | B、70° |
| C、100° | D、110° |
 已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AD=CD=6,BC=8.连接BD,AE⊥BD垂足为E.
已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AD=CD=6,BC=8.连接BD,AE⊥BD垂足为E. 已知:如图,AD∥BC,E是线段CD的中点,AE平分∠BAD.求证:BE平分∠ABC.
已知:如图,AD∥BC,E是线段CD的中点,AE平分∠BAD.求证:BE平分∠ABC. 如图为排水管的横截面,若此管道的半径为54cm,水面以上部分的弧长为27πcm 求横截面有水部分的面积.
如图为排水管的横截面,若此管道的半径为54cm,水面以上部分的弧长为27πcm 求横截面有水部分的面积.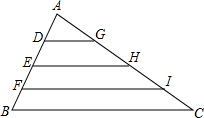 如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=6,则DG+EH+FI的长是
如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=6,则DG+EH+FI的长是