题目内容
20.计算:$\frac{\frac{1}{2}-\frac{1}{4}+\frac{1}{6}-\frac{1}{8}+\frac{1}{10}-\frac{1}{12}+…+\frac{1}{198}-\frac{1}{200}}{\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+…+\frac{1}{100}}$=$\frac{1}{2}$.分析 首先把分子减号变为加号,再减去所有负数的2倍,进一步计算整理和分母约分得出答案即可.
解答 解:∵原式的分子=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{8}$+$\frac{1}{10}$+…+$\frac{1}{198}$+$\frac{1}{200}$-2($\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{12}$+…+$\frac{1}{198}$+$\frac{1}{200}$)
=$\frac{1}{2}$×[(1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{99}$+$\frac{1}{100}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{49}$+$\frac{1}{50}$)]
=$\frac{1}{2}$×($\frac{1}{51}$+$\frac{1}{52}$+$\frac{1}{53}$+…+$\frac{1}{100}$),
∴原式=$\frac{\frac{1}{2}×(\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+…+\frac{1}{100})}{\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+…+\frac{1}{100}}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查有理数的混合运算,抓住数字的特点,灵活变形,巧算得出答案即可.

练习册系列答案
相关题目
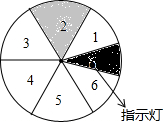 如图,将一个圆盘六等分,并把六个区域分别标上1,2,3,4,5,6,只有区域2为感应区域,中心角为30°的扇形AOB绕点O转动,在其半径OB上装有带指示灯的感应装置,当扇形AOB与区域2有重叠(O点除外)的部分时,指示灯会发光,否则不发光,当扇形ABO任意转动时,指示灯发光的概率为$\frac{1}{4}$.
如图,将一个圆盘六等分,并把六个区域分别标上1,2,3,4,5,6,只有区域2为感应区域,中心角为30°的扇形AOB绕点O转动,在其半径OB上装有带指示灯的感应装置,当扇形AOB与区域2有重叠(O点除外)的部分时,指示灯会发光,否则不发光,当扇形ABO任意转动时,指示灯发光的概率为$\frac{1}{4}$.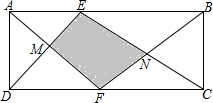 如图,长方形ABCD中,E、F分别是AB、DC上的点,AF、DE交于点M,BF、CE交于点N,若S△ADM=3cm2,S△BCN=4cm2,求阴影部分的面积.
如图,长方形ABCD中,E、F分别是AB、DC上的点,AF、DE交于点M,BF、CE交于点N,若S△ADM=3cm2,S△BCN=4cm2,求阴影部分的面积. 如图,正方形ABCD的边长为4,点P是对角线BD的上一点,PE⊥BC于点E,PF⊥CD于点F,则PA+PE+PF的最小值是4+2$\sqrt{2}$.
如图,正方形ABCD的边长为4,点P是对角线BD的上一点,PE⊥BC于点E,PF⊥CD于点F,则PA+PE+PF的最小值是4+2$\sqrt{2}$. 如图所示,△ABC中,AE,CD分别为△ABC的高,若AB=5cm,AE=4cm,CD=3cm,求BC的长.
如图所示,△ABC中,AE,CD分别为△ABC的高,若AB=5cm,AE=4cm,CD=3cm,求BC的长. 已知,如图,△ABC的内角∠ABC、∠ACB的角平分线交于点O,求∠BOC与∠A的关系.
已知,如图,△ABC的内角∠ABC、∠ACB的角平分线交于点O,求∠BOC与∠A的关系.