Question

10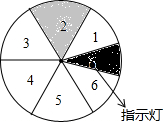．如图，将一个圆盘六等分，并把六个区域分别标上1，2，3，4，5，6，只有区域2为感应区域，中心角为30°的扇形AOB绕点O转动，在其半径OB上装有带指示灯的感应装置，当扇形AOB与区域2有重叠（O点除外）的部分时，指示灯会发光，否则不发光，当扇形ABO任意转动时，指示灯发光的概率为$\frac{1}{4}$．

Answer 1

分析 假设扇形区域逆时针转动，当OA越过OD时，指示灯开始发光，当OB越过OC时，指示灯停止发光，求出此过程中扇形转过的角度，据此可计算出指示灯发光的概率．

解答 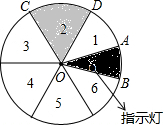解：如图，∵当扇形AOB落在区域2时，指示灯会发光；
假设扇形区域逆时针转动，当OA越过OD时，指示灯开始发光，当OB越过OC时，指示灯停止发光，
此过程中扇形转过的角度为：30°+60°=90°．
∴指示灯发光的概率为：$\frac{90}{360}$=$\frac{1}{4}$．
故答案为：$\frac{1}{4}$．

点评 本题主要考查了几何概率，用到的知识点为：概率=所求情况数与总情况数之比．得到指示灯发光的区域是解题的关键．