题目内容
 如图,Rt△ABC中,AB=AC,BD平分∠ABC交AC于点D,过点C作CE⊥BD,交BD的延长线于点E,连接AE.若AE=1,则BE的长为
如图,Rt△ABC中,AB=AC,BD平分∠ABC交AC于点D,过点C作CE⊥BD,交BD的延长线于点E,连接AE.若AE=1,则BE的长为考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:过A作AF⊥AE,易证∠ABD=∠DCE,∠BAF=∠CAE,即可证明△ABF和△ACE,可得AE=AF,即可求得AF=BF,即可解题.
解答: 解:过A作AF⊥AE,
解:过A作AF⊥AE,
∵∠ABD+∠ADB=90°,∠CDE+∠DCE=90°,∠ADB=∠CDE,
∴∠ABD=∠DCE,
∵∠BAF+∠CAF=90°,∠CAE+∠CAF=90°,
∴∠BAF=∠CAE,
在△ABF和△ACE中,
,
∴△ABF和△ACE,(ASA)
∴AE=AF,
∴∠AFE=45°,EF=
AE,
∵∠ABF=
∠ABC=22.5°,
∴∠BAF=∠ABF=22.5°,
∴AF=BF,
∴BE=(
+1)AE=
+1.
 解:过A作AF⊥AE,
解:过A作AF⊥AE,∵∠ABD+∠ADB=90°,∠CDE+∠DCE=90°,∠ADB=∠CDE,
∴∠ABD=∠DCE,
∵∠BAF+∠CAF=90°,∠CAE+∠CAF=90°,
∴∠BAF=∠CAE,
在△ABF和△ACE中,
|
∴△ABF和△ACE,(ASA)
∴AE=AF,
∴∠AFE=45°,EF=
| 2 |
∵∠ABF=
| 1 |
| 2 |
∴∠BAF=∠ABF=22.5°,
∴AF=BF,
∴BE=(
| 2 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABF和△ACE是解题的关键.

练习册系列答案
相关题目
某零件加工厂的生产车间要生产x个零件,原计划每天生产400个两件,实际生产时为了供货需要,每天多生产了100个零件,则完成生产x个零件可提前( )
A、(
| ||||
B、
| ||||
C、(
| ||||
D、
|
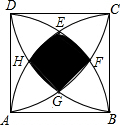 如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为( )
如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为( )A、
| ||
B、
| ||
| C、π | ||
D、
|
 “三月三,放风筝”,这天,妈妈让小玉自己动手制作一个如图所示的小风筝,它由两个三角形拼成,而且要满足△ABC≌△ADE才符合要求,小玉通过测量得到AB=AD,∠BAE=∠DAC,为了保证符合要求,还需要测量哪一对相等的量?请你帮助小玉找出一对相等的量并说明理由.
“三月三,放风筝”,这天,妈妈让小玉自己动手制作一个如图所示的小风筝,它由两个三角形拼成,而且要满足△ABC≌△ADE才符合要求,小玉通过测量得到AB=AD,∠BAE=∠DAC,为了保证符合要求,还需要测量哪一对相等的量?请你帮助小玉找出一对相等的量并说明理由.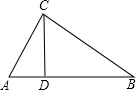 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AD=1,BD=4,求AC的长.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AD=1,BD=4,求AC的长. 如图,点O时直线AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中和为180°的两个角共有多少对?
如图,点O时直线AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中和为180°的两个角共有多少对?