题目内容
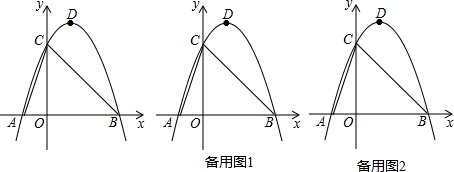
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,分析图象可知:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,分析图象可知:当k
当k
当k
考点:抛物线与x轴的交点
专题:
分析:此题实际上是求直线y=k与抛物线y=ax2+bx+c(a≠0)的交点问题,根据题意作出图形,根据图形直接回答问题.
解答: 解:如图,当k=2时,直线y=k与抛物线y=ax2+bx+c(a≠0)有一个交点,即方程ax2+bx+c=k有两个相等实数根;
解:如图,当k=2时,直线y=k与抛物线y=ax2+bx+c(a≠0)有一个交点,即方程ax2+bx+c=k有两个相等实数根;
当k<2时,直线y=k与抛物线y=ax2+bx+c(a≠0)有两个交点,即方程ax2+bx+c=k有两个不相等实数根;
当k>2时,直线y=k与抛物线y=ax2+bx+c(a≠0)没有交点,即方程ax2+bx+c=k没有实数根;
故答案是:=2;<2;>2.
 解:如图,当k=2时,直线y=k与抛物线y=ax2+bx+c(a≠0)有一个交点,即方程ax2+bx+c=k有两个相等实数根;
解:如图,当k=2时,直线y=k与抛物线y=ax2+bx+c(a≠0)有一个交点,即方程ax2+bx+c=k有两个相等实数根;当k<2时,直线y=k与抛物线y=ax2+bx+c(a≠0)有两个交点,即方程ax2+bx+c=k有两个不相等实数根;
当k>2时,直线y=k与抛物线y=ax2+bx+c(a≠0)没有交点,即方程ax2+bx+c=k没有实数根;
故答案是:=2;<2;>2.
点评:本题考查了抛物线与x轴的交点问题.利用数形结合的数学思想解题,使问题变得直观化,降低了题的难度.

练习册系列答案
相关题目
在平面直角坐标系中,点P(-3,2013)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若m与n为正整数,xm+yn+2m+n的次数是( )
| A、m | B、n |
| C、m+n | D、m,n中较大的数 |
下列方程中是一元二次方程的是( )
| A、(x-1)(2x+3)=2x(x+1) | ||
| B、ax2+bx+c=0 | ||
C、4x-
| ||
| D、(2a+3)(4a-1)=0 |
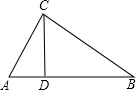 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AD=1,BD=4,求AC的长.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AD=1,BD=4,求AC的长. 如图,点O时直线AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中和为180°的两个角共有多少对?
如图,点O时直线AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中和为180°的两个角共有多少对?