题目内容
用公式法解下列方程.
(1)x2+x-12=0
(2)x2-
x-
=0
(3)x2+4x+8=2x+11
(4)x(x-4)=2-8x
(5)x2+2x=0
(6)x2+2
x+10=0.
(1)x2+x-12=0
(2)x2-
| 2 |
| 1 |
| 4 |
(3)x2+4x+8=2x+11
(4)x(x-4)=2-8x
(5)x2+2x=0
(6)x2+2
| 5 |
考点:解一元二次方程-公式法
专题:
分析:(1)(2)(5)(6)首先确定a、b、c的值,然后计算△的值,判断△的符号,当△≥0时,利用求根公式即可求解;
(3)(4)首先把方程化成一般形式,然后利用求根公式求解.
(3)(4)首先把方程化成一般形式,然后利用求根公式求解.
解答:解:(1)a=1,b=1,c=-12,
△=1-4×1×(-12)=49>0,
故x=
,
则x1=-4,x2=3;
(2)a=1,b=-
,c=-
,
△=2+1=3,
故x=
,
则x1=
,x2=
;
(3)原式即:x2+2x-3=0,
则a=1,b=2,c=-3,
△=4+12=16>0,
故x=
,
则x1=1,x2=-3;
(4)原式即:x2+4x-2=0,
a=1,b=4,c=-2,
△=16-4×1×(-2)=24>0,
故x=
,
则x1=-2+
,x2=-2-
;
(5)a=1,b=2,c=0,
△=4>0,
故x=
,
则x1=-2,x2=0;
(6)a=1,b=2
,c=10,
△=(2
)2-40=-20<0,
则方程没有实数解.
△=1-4×1×(-12)=49>0,
故x=
| -1±7 |
| 2 |
则x1=-4,x2=3;
(2)a=1,b=-
| 2 |
| 1 |
| 4 |
△=2+1=3,
故x=
| ||||
| 2 |
则x1=
| ||||
| 2 |
| ||||
| 2 |
(3)原式即:x2+2x-3=0,
则a=1,b=2,c=-3,
△=4+12=16>0,
故x=
-2±
| ||
| 2 |
则x1=1,x2=-3;
(4)原式即:x2+4x-2=0,
a=1,b=4,c=-2,
△=16-4×1×(-2)=24>0,
故x=
-4±
| ||
| 2 |
则x1=-2+
| 6 |
| 6 |
(5)a=1,b=2,c=0,
△=4>0,
故x=
-2±
| ||
| 2 |
则x1=-2,x2=0;
(6)a=1,b=2
| 5 |
△=(2
| 5 |
则方程没有实数解.
点评:本题考查了一元二次方程的求根公式,正确记忆求根公式是关键.

练习册系列答案
相关题目
 直线l1:y=kx+b过点B(5,-1)且平行于直线y=-x.
直线l1:y=kx+b过点B(5,-1)且平行于直线y=-x.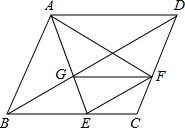 在菱形ABCD中点EF分别在BC、CD上,AE交BD于G,连结AF、EF,EF∥BD.
在菱形ABCD中点EF分别在BC、CD上,AE交BD于G,连结AF、EF,EF∥BD. 如图,已知AC、BD相交于点O,∠ADC=∠BCD,∠1=∠2,AD=BC,求证:△AOD≌△BOC.
如图,已知AC、BD相交于点O,∠ADC=∠BCD,∠1=∠2,AD=BC,求证:△AOD≌△BOC.