题目内容
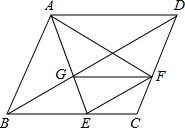 在菱形ABCD中点EF分别在BC、CD上,AE交BD于G,连结AF、EF,EF∥BD.
在菱形ABCD中点EF分别在BC、CD上,AE交BD于G,连结AF、EF,EF∥BD.(1)求证:∠BAE=∠DAF;
(2)若又有GF∥BC,求BG:DG的值.
考点:菱形的性质
专题:
分析:(1)通过全等三角形的判定定理SAS证得△ABE≌△ADF,则该全等三角形的对应角相等:∠BAE=∠DAF;
(2)设BG=x,GD=y,DF=a,FC=b,则BE=GF=a,AD=DC=a+b.根据平行线分线段成比例来求BG:DG的值.
(2)设BG=x,GD=y,DF=a,FC=b,则BE=GF=a,AD=DC=a+b.根据平行线分线段成比例来求BG:DG的值.
解答:(1)证明:∵四边形ABCD是菱形,
∴AB=AD=BC=CD,∠ABE=∠ADF,
∵EF∥BD,
∴CE=CF,
∴BE=DF,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF;
(2)设BG=x,GD=y,DF=a,FC=b,则BE=GF=a,AD=DC=a+b
∵GF∥BC,
∴BG:GD=CF:DF,
∴X:Y=b:a
∵BE∥AD,
∴BG:GD=BE:AD,
∴X:Y=a:(a+b)
∴b:a=a:(a+b)
∴a2-ab-b2=0
(
)2-
-1=0
∴
=
或(
=
舍弃)
∴BG:DG=(
-1):2.
∴AB=AD=BC=CD,∠ABE=∠ADF,
∵EF∥BD,
∴CE=CF,
∴BE=DF,
在△ABE和△ADF中,
|
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF;
(2)设BG=x,GD=y,DF=a,FC=b,则BE=GF=a,AD=DC=a+b

∵GF∥BC,
∴BG:GD=CF:DF,
∴X:Y=b:a
∵BE∥AD,
∴BG:GD=BE:AD,
∴X:Y=a:(a+b)
∴b:a=a:(a+b)
∴a2-ab-b2=0
(
| b |
| a |
| b |
| a |
∴
| b |
| a |
| ||
| 2 |
| ||
| 2 |
| b |
| a |
-
| ||
| 2 |
∴BG:DG=(
| 5 |
点评:本题是简单的推理证明题,主要考查菱形的边的性质,同时综合利用全等三角形的判定方法及平行线分线段成比例的性质.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
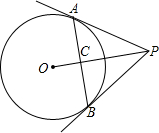 如图,PA,PB分别切圆O于点A,B,圆O的半径为
如图,PA,PB分别切圆O于点A,B,圆O的半径为 如图,△ABC中,AC>AB,AD平分角BAC,BD⊥AD,E是BC的中点,若DE=2,则AC-AB=
如图,△ABC中,AC>AB,AD平分角BAC,BD⊥AD,E是BC的中点,若DE=2,则AC-AB=