题目内容
 直线l1:y=kx+b过点B(5,-1)且平行于直线y=-x.
直线l1:y=kx+b过点B(5,-1)且平行于直线y=-x.(1)求直线l1的解析式;
(2)若直线l2:y=2x-2与直线l1交于点A,与y轴交于点C,求由O、A、B、C四点所构成的四边形的面积;
(3)若有一条经过原点的直线l3,恰好平分四边形OABC的面积,试求此直线l3的解析式.
考点:两条直线相交或平行问题
专题:
分析:(1)先根据y=kx+b与直线y=2x平行求出k的值,再根据B(5,-1)求出b的值即可.
(2)先求得C的坐标,直线AB的解析式从而求得与x轴的交点D的坐标,根据四边形的面积=S△AOD+S△BOD+S△OBC即可求得;
(3)根据三角形的面积求得直线l3与直线AB的交点的纵坐标,代入直线AB的解析式求得横坐标,设直线l3的解析式为y=kx,把交点坐标代入即可.
(2)先求得C的坐标,直线AB的解析式从而求得与x轴的交点D的坐标,根据四边形的面积=S△AOD+S△BOD+S△OBC即可求得;
(3)根据三角形的面积求得直线l3与直线AB的交点的纵坐标,代入直线AB的解析式求得横坐标,设直线l3的解析式为y=kx,把交点坐标代入即可.
解答: 解:由题意得,(1)∵直线y=kx+b与直线y=-x平行,
解:由题意得,(1)∵直线y=kx+b与直线y=-x平行,
∴k=-1,
设此一次函数的解析式为:y=-x+b,
∵直线l1:y=kx+b过点B(5,-1),
∴-1=-5+b,
解得:b=4,
∴直线l1的解析式为:y=-x+4;
(2)解
得
,
∴A(2,2);
由直线l2:y=2x-2可知:C(0,-2),
∴直线AB为:y=-x+4,
∴直线AB与x轴的交点为D(4,0),
∴由O、A、B、C四点所构成的四边形的面积=S△AOD+S△BOD+S△OBC=
OD•2+
OD•1+
OC•5=
×4×2+
×4×1+
×2×5=11;
(3)设直线l3交直线AB于E,
∵S△AOD=
OD•2=
×4×2=4,四边形OABC的面积=11,
∴S△ODE=
-4=
,
设E的纵坐标为h,
∴S△ODE=
OD•h=
,
∴h=
×2×
=
,
∴E的纵坐标为-
,
代入直线AB解析式y=-x+4,得x=
,
∵经过原点的直线l3,
∴设直线l3为y=kx,
∴-
=
k,解得k=-
,
∴直线l3的解析式为y=-
x;
 解:由题意得,(1)∵直线y=kx+b与直线y=-x平行,
解:由题意得,(1)∵直线y=kx+b与直线y=-x平行,∴k=-1,
设此一次函数的解析式为:y=-x+b,
∵直线l1:y=kx+b过点B(5,-1),
∴-1=-5+b,
解得:b=4,
∴直线l1的解析式为:y=-x+4;
(2)解
|
|
∴A(2,2);
由直线l2:y=2x-2可知:C(0,-2),
∴直线AB为:y=-x+4,
∴直线AB与x轴的交点为D(4,0),
∴由O、A、B、C四点所构成的四边形的面积=S△AOD+S△BOD+S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)设直线l3交直线AB于E,
∵S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ODE=
| 11 |
| 2 |
| 3 |
| 2 |
设E的纵坐标为h,
∴S△ODE=
| 1 |
| 2 |
| 3 |
| 2 |
∴h=
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
∴E的纵坐标为-
| 3 |
| 4 |
代入直线AB解析式y=-x+4,得x=
| 19 |
| 4 |
∵经过原点的直线l3,
∴设直线l3为y=kx,
∴-
| 3 |
| 4 |
| 19 |
| 4 |
| 3 |
| 19 |
∴直线l3的解析式为y=-
| 3 |
| 19 |
点评:本题考查了两直线平行时系数k的关系,四边形的面积、方程的解以及函数与坐标轴的交点的综合应用,正确求得四边形OABC的面积是关键.

练习册系列答案
相关题目
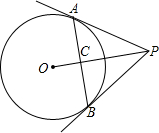 如图,PA,PB分别切圆O于点A,B,圆O的半径为
如图,PA,PB分别切圆O于点A,B,圆O的半径为 如图,AB=AE,AC=AD,BD=CE.求证:∠CAB=∠DAE.
如图,AB=AE,AC=AD,BD=CE.求证:∠CAB=∠DAE.