题目内容
4.抛物线y=-x2+bx+c的顶点为Q,与x轴交于A(-1,0)、B(5,0)两点,与y轴交于点C.求抛物线的解析式及其顶点Q的坐标.分析 把点A、B的坐标代入抛物线解析式求出b、c的值,即可得到抛物线解析式,然后整理成顶点式形式,再写出顶点坐标即可.
解答 解:∵抛物线y=-x2+bx+c经过点A(-1,0)、B(5,0),
∴$\left\{\begin{array}{l}{-1-b+c=0}\\{-25+5b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=4}\\{c=5}\end{array}\right.$,
∴抛物线的解析式为y=-x2+4x+5,
∵y=-x2+4x+5=-(x-2)2+9,
∴Q(2,9).
点评 本题考查了待定系数法求二次函数的解析式,熟练掌握待定系数法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.比较3115和769的大小关系是( )
| A. | 3115>769 | B. | 3115<769 | C. | 3115=769 | D. | 无法判定 |
12.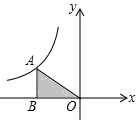 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )
 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )| A. | $y=-\frac{2}{x}$ | B. | $y=\frac{2}{x}$ | C. | $y=-\frac{4}{x}$ | D. | $y=\frac{4}{x}$ |
9.下列每组数据中的三个数值分别为三角形的三边长,不能构成直角三角形是( )
| A. | 4,6,8 | B. | 9,40,41 | C. | 5,12,13 | D. | 7,24,25 |
16.下列命题中,是真命题的( )
| A. | 同一平面内,两条直线一定互相平行 | |
| B. | 若a∥b,b∥c,则a∥c | |
| C. | 若a 2=b 2,则a=b | |
| D. | 从直线外一点到这条直线的垂线段,叫做点到直线的距离 |
6.某支骨片上周末的收盘价格是每股10元.本周一到周五的收盘情况如下:
(“+”表示股票比前一天上涨,“-”表示股票比前一天下跌)
(1)这五天中哪天收盘价格最高?哪天收盘价格最低?最高与最低相差多少?
(2)买进股票时需付成交额0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税.小明哥在上周末以每股10元的价格买进2000股,然后再星期三收盘结束时将股票全部卖出,他的收益如何?
(“+”表示股票比前一天上涨,“-”表示股票比前一天下跌)
| 上周末收盘价 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 10 | +4.5 | -1.5 | +3 | -2.5 | -5 |
(2)买进股票时需付成交额0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税.小明哥在上周末以每股10元的价格买进2000股,然后再星期三收盘结束时将股票全部卖出,他的收益如何?
7.一元二次方程x2-2x=3的二次项系数、一次项系数、常数项分别是( )
| A. | 1、2、-3 | B. | 1、2、3 | C. | 1、-2、3 | D. | 1、-2、-3 |
 某台风中心在A城正南方向100km处,以20km/h的速度向A城移动,此时一辆汽车从A城以60km/h的速度向正西方向行驶.则这辆汽车与台风中心的最近距离为30$\sqrt{10}$km.
某台风中心在A城正南方向100km处,以20km/h的速度向A城移动,此时一辆汽车从A城以60km/h的速度向正西方向行驶.则这辆汽车与台风中心的最近距离为30$\sqrt{10}$km.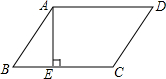 如图,平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,求平行四边形ABCD的周长.
如图,平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,求平行四边形ABCD的周长.