题目内容
6.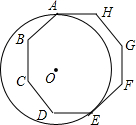 如图,⊙O与正八边形ABCDEFGH的边AH,EF相切于点A,E.若⊙O的半径为4,则劣弧$\widehat{AE}$的长为3π.
如图,⊙O与正八边形ABCDEFGH的边AH,EF相切于点A,E.若⊙O的半径为4,则劣弧$\widehat{AE}$的长为3π.
分析 连接OA、OE,由切线的性质得出∠OAE=∠OEF=90°,求出正八边形的内角∠H=∠G=∠F=135°,由六边形内角和求出∠AOE的度数,再由弧长公式即可得出劣弧$\widehat{AE}$的长.
解答 解:连接OA、OE,如图所示: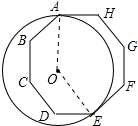
∵⊙O与AH,EF相切于点A,E,
∴AH⊥OA,EF⊥OE,
∴∠OAE=∠OEF=90°,
∵在正八边形ABCDEFGH中,∠H=∠G=∠F=(8-2)×180°÷8=135°,
∴∠AOE=(6-2)×180°-90°-90°-3×135°=135°,
∴劣弧$\widehat{AE}$的长=$\frac{135×π×4}{180}$=3π;
故答案为:3π.
点评 本题考查了切线的性质、正多边形和圆的关系、多边形内角和定理、弧长公式;熟练掌握切线的性质和多边形内角和定理,通过作辅助线求出∠AOE是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列各组数的比较大小中,不正确的是( )
| A. | -$\frac{6}{5}>-(-\frac{3}{5})$ | B. | -(+3)<-(-4) | C. | 0>-|-3| | D. | +(-2)<-(-1) |
17.已知$\frac{1}{x}+\frac{1}{y}$=$\frac{4}{3}$,则$\frac{xy}{3(x+y)}$的值为( )
| A. | $\frac{9}{4}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
16.用配方法解方程x2-4x+2=0,下列配方正确的是( )
| A. | (x-4)2=14 | B. | (x+4)2=14 | C. | (x+2)2=2 | D. | (x-2)2=2 |
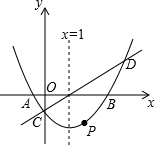 如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点.
如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点. 如图,梯形ABCD中,AD∥BC,AC⊥BD,垂足为H,∠DBE=∠CBE,BD=BC,求证:FH•AC=FC2+FC•FH.
如图,梯形ABCD中,AD∥BC,AC⊥BD,垂足为H,∠DBE=∠CBE,BD=BC,求证:FH•AC=FC2+FC•FH.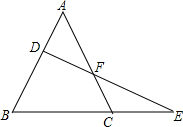 如图,△ABC中,直线DE交AB于D,交AC于F,交BC的延长线于E,求证:$\frac{AD}{DB}$•$\frac{BE}{EC}$•$\frac{CF}{FA}$=1.
如图,△ABC中,直线DE交AB于D,交AC于F,交BC的延长线于E,求证:$\frac{AD}{DB}$•$\frac{BE}{EC}$•$\frac{CF}{FA}$=1.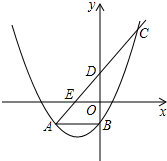 如图,抛物线y=ax2+2ax+c与直线y=x+b交于A(-2,-1)、C(1,2)两点,与y轴交于B,D、E是直线y=x+b与坐标轴的交点,
如图,抛物线y=ax2+2ax+c与直线y=x+b交于A(-2,-1)、C(1,2)两点,与y轴交于B,D、E是直线y=x+b与坐标轴的交点,