题目内容
3．等腰三角形的一边长为9，另一边长为6，则此三角形的周长是24或21．分析 分边9是底边和腰长两种情况讨论，再根据三角形的任意两边之和大于第三边判断是否能组成三角形，然后求解即可．
解答 解：若9是底边，则三角形的三边分别为9、6、6，
能组成三角形，周长=9+6+6=21，
若9是腰长，则三角形的三边分别为9、9、6，
能组成三角形，周长=9+9+6=24，
综上所述，此三角形的周长是24或21．
故答案为：24或21．
点评 本题考查了等腰三角形的性质，三角形的三边关系，难点在于分情况讨论并判断是否能组成三角形．
练习册系列答案
名校课堂系列答案
相关题目
13．
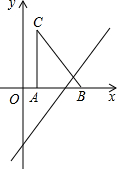如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标分别为（1，0）、（4，0）．将△ABC沿x轴向右平移，当点C落在直线y=2x-6上时，线段BC扫过的面积为（ ）
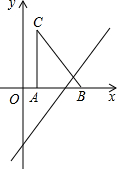如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标分别为（1，0）、（4，0）．将△ABC沿x轴向右平移，当点C落在直线y=2x-6上时，线段BC扫过的面积为（ ）| A． | 4 | B． | 8 | C． | 16 | D． | 8$\sqrt{2}$ |
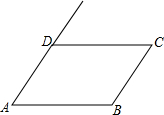如图所示：已知AD∥BC，∠A=∠C．
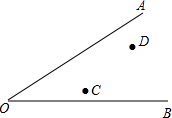如图，C、D是∠AOB内部两点，在∠AOB内部求作一点P，使PC=PD，并且使点P到∠AOB两边的距离相等（要求：不写作法，保留作图痕迹）
8．
如图，AB=AC，BE平分∠ABC，DE∥BC，图中等腰三角形共有（ ）
如图，AB=AC，BE平分∠ABC，DE∥BC，图中等腰三角形共有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
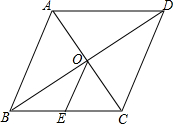如图，菱形ABCD的对角线AC、BD交于点O，AC=6cm，BD=8cm，点E是边BC的中点，连接OE，则OE=2.5cm．
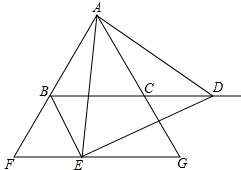如图：△ABC是等边三角形，点D是射线BC上的一个动点（点D不与点B、C重合），△ADE是以AD为边的等边三角形，过点E作BC的平行线，分别交射线AB、AC于点F、G，连接BE．