题目内容
如图，点G是△ABC的重心，过G作EF∥AB，分别交AC，BC于点E，F，作ED∥BC，交AB于点D，若四边形BFED的面积为12，求S△ABC．考点：三角形的重心
专题：
分析：连接CG并延长，交AB于H，过点F作FN⊥AB于N，过点C作CM⊥AB于M，由点G是△ABC的重心可得BH=AH，且CG=
CH．易证△CGF∽△CHB，△CGE∽△CHA，△BNF∽△BMC，然后根据相似三角形的性质可求出
、
，从而可求出
，根据条件就可求出△ABC的面积．
| 2 |
| 3 |
| EF |
| AB |
| FN |
| CM |
| S四边形BFED |
| S△ABC |
解答：解：连接CG并延长，交AB于H，过点F作FN⊥AB于N，过点C作CM⊥AB于M，如图，
则有CM∥FN．
∵点G是△ABC的重心，
∴BH=AH，且CG=
CH．
∵EF∥AB，
∴△CGF∽△CHB，△CGE∽△CHA，
∴
=
=
=
，
=
=
，
∴
=
，
=1-
=
．
∵BH=AH，
∴GF=GE，
∴
=
=
．
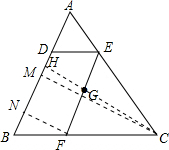
∵CM∥FN，
∴△BNF∽△BMC，
∴
=
=
．
∵EF∥AB，ED∥BC，
∴四边形BFED是平行四边形，
∴EF=DB，
∴
=
=
=2×
×
=
．
∵S四边形BFED=12，
∴S△ABC=27．
则有CM∥FN．
∵点G是△ABC的重心，
∴BH=AH，且CG=
| 2 |
| 3 |
∵EF∥AB，
∴△CGF∽△CHB，△CGE∽△CHA，
∴
| GF |
| HB |
| CF |
| CB |
| CG |
| CH |
| 2 |
| 3 |
| GE |
| HA |
| CG |
| CH |
| 2 |
| 3 |
∴
| GF |
| HB |
| GE |
| HA |
| BF |
| BC |
| CF |
| CB |
| 1 |
| 3 |
∵BH=AH，
∴GF=GE，
∴
| EF |
| AB |
| 2GF |
| 2HB |
| 2 |
| 3 |
∵CM∥FN，
∴△BNF∽△BMC，
∴
| FN |
| CM |
| BF |
| BC |
| 1 |
| 3 |
∵EF∥AB，ED∥BC，
∴四边形BFED是平行四边形，
∴EF=DB，
∴
| S四边形BFED |
| S△ABC |
| DB•FN | ||
|
| 2EF•FN |
| AB•CM |
=2×
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
∵S四边形BFED=12，
∴S△ABC=27．
点评：本题主要考查了相似三角形的判定与性质、平行四边形的判定与性质、三角形重心等知识，利用重心的性质分别求出四边形BFED与△ABC底的比、高的比是解决本题的关键．
练习册系列答案
相关题目
图中同旁内角有多少对？请逐一写出来．
如图，直线y=kx+b与y轴的交点坐标为A（0，1），与x轴的标点坐标为B（-3，0），P，Q分别是射线BO和射线BA上的动点． 
2002年8月在北京召开的国际数学家大会的会徽取材于我国古代数学家赵爽的《勾股圆方图》它是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形，如图，若大正方形的面积是64，一个直角三角形两直角边长和为10，则小正方形的面积为
如图所示，OE，OD分别平分∠AOC和∠BOC，