题目内容
有若干个数a1、a2,a3,…,an,若a1=-
,从第二个数起,每个数都等于“1与它前面的那个数差的倒数”.
(1)求a2= ;a3= ;
(2)求a9•a10•a11的值;
(3)是否存在M的值,使M÷(an-1•an•an+1)=a1?若存在,请求出M的值.
| 1 |
| 2 |
(1)求a2=
(2)求a9•a10•a11的值;
(3)是否存在M的值,使M÷(an-1•an•an+1)=a1?若存在,请求出M的值.
考点:规律型:数字的变化类
专题:
分析:(1)将各个数字依次计算,因为a1=-
,得出a2=
,a3=
,进而得出答案;
(2)根据题意得出a4=
,故得出这些数字不断重复出现,周期为3,从而求解;
(3)利用an-1•an•an+1,为连续三个数,进而得出an-1.an.an+1=-1,进而得出答案.
| 1 |
| 2 |
| 1 | ||
1-(-
|
| 1 | ||
1-
|
(2)根据题意得出a4=
| 1 |
| 1-3 |
(3)利用an-1•an•an+1,为连续三个数,进而得出an-1.an.an+1=-1,进而得出答案.
解答:解:(1)由题意可得:∵a1=-
,
∴a2=
=
,a3=
=3;
故答案为:
,3;
(2)由题意可得:a4=
=-
,则a的值每3个一循环,
故a9=a3,a10=a1,a11=a2,
则a9•a10•a11=-
×
×3=-1;
(3)从该题可以看出,an-1•an•an+1,为连续三个数,从第一问中我们已经得出结论,
任意三个连续的数字,它们三个数字均为-
,
,3,只不过排列顺序不同而已.
因此,这三个数字相乘,得出的结果是:an-1.an.an+1=-1.又已知A1=-
,
所以,利用倒推法,由-
×(-1)=
,
故这个M值存在,它的值为
.
| 1 |
| 2 |
∴a2=
| 1 | ||
1-(-
|
| 2 |
| 3 |
| 1 | ||
1-
|
故答案为:
| 2 |
| 3 |
(2)由题意可得:a4=
| 1 |
| 1-3 |
| 1 |
| 2 |
故a9=a3,a10=a1,a11=a2,
则a9•a10•a11=-
| 1 |
| 2 |
| 2 |
| 3 |
(3)从该题可以看出,an-1•an•an+1,为连续三个数,从第一问中我们已经得出结论,
任意三个连续的数字,它们三个数字均为-
| 1 |
| 2 |
| 2 |
| 3 |
因此,这三个数字相乘,得出的结果是:an-1.an.an+1=-1.又已知A1=-
| 1 |
| 2 |
所以,利用倒推法,由-
| 1 |
| 2 |
| 1 |
| 2 |
故这个M值存在,它的值为
| 1 |
| 2 |
点评:此题主要考查了数字变化类,根据题意得出a的变化规律是解题关键.

练习册系列答案
相关题目
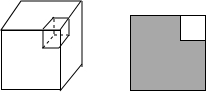 如图所示,在边长为a的正方形中减去一个边长为b的小正方形(a>b),剩下的部分的面积,可得到平方差公式;那么在边长a的正方体中减去一个边长为b的小正方体(a>b),剩下的部分的体积为a3-b3,它等于( )
如图所示,在边长为a的正方形中减去一个边长为b的小正方形(a>b),剩下的部分的面积,可得到平方差公式;那么在边长a的正方体中减去一个边长为b的小正方体(a>b),剩下的部分的体积为a3-b3,它等于( )| A、(a+b)(a2-ab+b2) |
| B、(a-b)(a2+ab+b2) |
| C、(a-b)(a2+b2) |
| D、(a+b)(a2-b2) |
下列调查中,适宜采用全面调查(普查)的是( )
| A、对全国中学生心理健康现状的调查 |
| B、对冷饮市场上冰淇淋质量情况的调查 |
| C、对西安市市民实施低碳生活情况的调查 |
| D、对“神舟九号”飞船零部件状况的检查 |
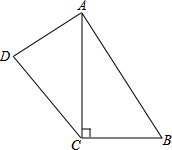 已知:四边形ABCD中,AC⊥BC,AB=17,BC=8,CD=12,DA=9.
已知:四边形ABCD中,AC⊥BC,AB=17,BC=8,CD=12,DA=9.
 如图所示,E是正方形ABCD的边BC上一点,F是DC的延长线上一点,且∠BAE=∠FAE,求证:BE+DF=AF.
如图所示,E是正方形ABCD的边BC上一点,F是DC的延长线上一点,且∠BAE=∠FAE,求证:BE+DF=AF. 如图,点G是△ABC的重心,过G作EF∥AB,分别交AC,BC于点E,F,作ED∥BC,交AB于点D,若四边形BFED的面积为12,求S△ABC.
如图,点G是△ABC的重心,过G作EF∥AB,分别交AC,BC于点E,F,作ED∥BC,交AB于点D,若四边形BFED的面积为12,求S△ABC.