题目内容
18.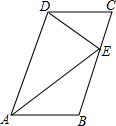 如图,在?ABCD中,点E在BC上,∠CDE=∠DAE.
如图,在?ABCD中,点E在BC上,∠CDE=∠DAE.(1)求证:△ADE∽△DEC;
(2)若AD=8,DE=4,求BE的长.
分析 (1)根据AD∥BC,可以证得∠ADE=∠DEC,然后根据∠CDE=∠DAE即可证得;
(2)根据相似三角形对应边的比相等,即可求得EC的长,则BE即可求解.
解答 解:
(1)∵?ABCD中,AD∥BC,
∴∠ADE=∠DEC,
又∵∠CDE=∠DAE,
∴△ADE∽△DEC;
(2)∵△ADE∽△DEC,
∴$\frac{DE}{AD}=\frac{EC}{DE}$,
∴$\frac{4}{8}=\frac{EC}{4}$,
∴EC=2,
又∵BC=AD=8,
∴BE=8-2=6.
点评 本题考查了相似三角形的判定与性质,证明两个三角形相似最常用的方法是证明两组角对应相等,熟练掌握平行四边形的各种性质是解题关键.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
2.甲、乙两人练习赛跑,甲每秒跑7米,乙每秒跑6.5米,甲让乙先跑5米,设x秒后甲可追上乙,则下列四个方程中不正确的是( )
| A. | 7x=6.5x+5 | B. | 7x+5=6.5x | C. | (7-6.5)x=5 | D. | 6.5x=7x-5 |
13.已知圆锥的底面半径是3,高是4,则这个圆锥的全面积是( )
| A. | 12π | B. | 15π | C. | 24π | D. | 30π |
8.用科学记数法表示108000000,正确的是( )
| A. | 1.08×108 | B. | 1.08×109 | C. | 10.8×107 | D. | 0.108×109 |
 矩形ABCD中,∠DBA=60°,把△ABD绕点B逆时针旋转使得点A落在BD上,点A对称点为点A1,点D对称点为点D1,A1 D1与BC交于点E,连接D1C.
矩形ABCD中,∠DBA=60°,把△ABD绕点B逆时针旋转使得点A落在BD上,点A对称点为点A1,点D对称点为点D1,A1 D1与BC交于点E,连接D1C. 如图,已知锐角三角形ABC.
如图,已知锐角三角形ABC.