题目内容
13.已知圆锥的底面半径是3,高是4,则这个圆锥的全面积是( )| A. | 12π | B. | 15π | C. | 24π | D. | 30π |
分析 先利用勾股定理计算出母线长,再利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长计算出圆锥的侧面积,然后计算侧面积与底面积的和即可.
解答 解:圆锥的母线长=$\sqrt{{3}^{2}+{4}^{2}}$=5,
所以这个圆锥的全面积=π•32+$\frac{1}{2}$•2π•3•5=24π.
故选C.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
17.若下列各组值代表线段的长度,能组成三角形的是( )
| A. | 1、2、3.5 | B. | 4、5、9 | C. | 5、15、8 | D. | 20、15、8 |
8.已知点M(2,-3),点N与点M关于x轴对称,则点N的坐标是( )
| A. | (-2,3) | B. | (-2,-3) | C. | (3,2) | D. | (2,3) |
5.下列各式运算正确的是( )
| A. | 3a+6b=9ab | B. | $\frac{1}{2}$y2-$\frac{1}{3}$y2=$\frac{1}{6}$ | C. | 8a4-6a3=2a | D. | 3a3b-3ba3=0 |
2.若a>0,b<-2,则点(a,b+2)在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
3.已知x2yn与-xmy3是同类项,则m+n=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
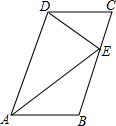 如图,在?ABCD中,点E在BC上,∠CDE=∠DAE.
如图,在?ABCD中,点E在BC上,∠CDE=∠DAE.