题目内容
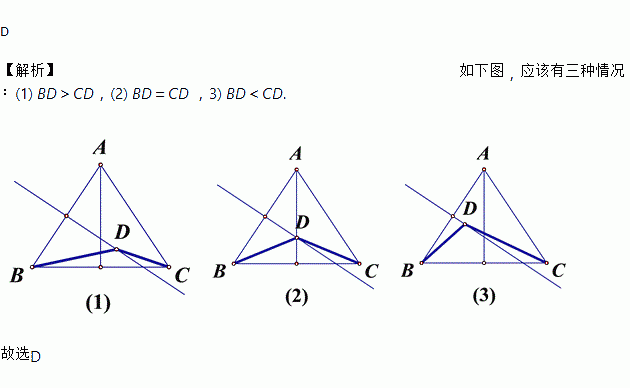
△ABC中,AB=AC,点D与顶点A在直线BC同侧,且BD=AD.则BD与CD的大小关系为( )
A. BD>CD B. BD=CD C. BD<CD D. BD与CD大小关系无法确定
 D
【解析】如下图,应该有三种情况:(1) BD>CD,(2) BD=CD ,3) BD<CD.
故选D
D
【解析】如下图,应该有三种情况:(1) BD>CD,(2) BD=CD ,3) BD<CD.
故选D
练习册系列答案
相关题目
(1)三角形的中位线的定义:连结三角形两边____________叫做三角形的中位线.
(2)三角形的中位线定理是三角形的中位线________第三边,并且等于___________.
 (1)中点的线段; (2)平行于三角形的 第三边的一半
【解析】(1)三角形的中位线的定义:连结三角形两边中点的线段叫做三角形的中位线,
故答案为:中点的线段;
(2)三角形的中位线定理是三角形的中位线平行于三角形的第三边,并且等于第三边的一半,
故答案为:平行于三角形的,第三边的一半.
(1)中点的线段; (2)平行于三角形的 第三边的一半
【解析】(1)三角形的中位线的定义:连结三角形两边中点的线段叫做三角形的中位线,
故答案为:中点的线段;
(2)三角形的中位线定理是三角形的中位线平行于三角形的第三边,并且等于第三边的一半,
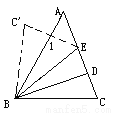
故答案为:平行于三角形的,第三边的一半. 如图,△ABC中,∠ A=500,∠C=700,BD、BE三等分∠ABC,将△BCE沿BE对折,点C落在C’处,则∠1=_________;
 90°
【解析】根据翻折求出各个角的度数,再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠1的度数.
【解析】
∵∠ A=500,∠C=700,
∴∠ABC =60°,
∵BD、BE三等分∠ABC,
∴∠ABE =∠EBD =∠DBC =20°,
∴∠EBC =∠EBD +∠DBC =40°,
由翻折得∠C’BE=∠EBC =40°, ∠C’ =...
90°
【解析】根据翻折求出各个角的度数,再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠1的度数.
【解析】
∵∠ A=500,∠C=700,
∴∠ABC =60°,
∵BD、BE三等分∠ABC,
∴∠ABE =∠EBD =∠DBC =20°,
∴∠EBC =∠EBD +∠DBC =40°,
由翻折得∠C’BE=∠EBC =40°, ∠C’ =... 两个图形关于某直线对称,对称点一定( )
A. 这直线的两旁 B. 这直线的同旁 C. 这直线上 D. 这直线两旁或这直线上
 D
【解析】由成轴对称的定义知,成轴对称的两个图形的对称点,或者在对称轴上,或者在对称轴两旁.
故选D.
D
【解析】由成轴对称的定义知,成轴对称的两个图形的对称点,或者在对称轴上,或者在对称轴两旁.
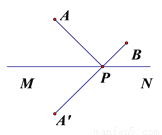
故选D. 如图,已知点A、B直线MN同侧两点, 点A’、A关于直线MN对称.连接A’B交直线MN于点P,连接AP.若A’B=5cm,则AP+BP的长为________
 5cm
【解析】∵点A′、A关于直线MN对称,点P在对称轴MN上,
∴A′P、AP关于直线MN对称,
∴A′P=AP,
∴AP+BP= A′P+PB=A′B=5cm.
5cm
【解析】∵点A′、A关于直线MN对称,点P在对称轴MN上,
∴A′P、AP关于直线MN对称,
∴A′P=AP,
∴AP+BP= A′P+PB=A′B=5cm. 轴对称图形沿对称轴对折后,对称轴两旁的部分( )
A. 完全重合 B. 不完全重合 C. 两者都有 D. 不确定
 A
【解析】由轴对称图形的定义知,轴对称图形沿对称轴对折后,对称轴两旁的部分完全重合.
故选A.
A
【解析】由轴对称图形的定义知,轴对称图形沿对称轴对折后,对称轴两旁的部分完全重合.
故选A. 下列说法中正确的有( )
①角的两边关于角平分线对称; ②两点关于连结它的线段的中垂线对称
③成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称
④到直线l距离相等的点关于l对称
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】①∵应该为角的两边关于“角平分线所在直线”对称,故不正确;
②“两点关于连结它的线段的中垂线对称”正确;
③“成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称”正确;
④∵到直线l距离相等的点可以在l的同一侧,故不正确;
∴②和③正确.
故选B.
B
【解析】①∵应该为角的两边关于“角平分线所在直线”对称,故不正确;
②“两点关于连结它的线段的中垂线对称”正确;
③“成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称”正确;
④∵到直线l距离相等的点可以在l的同一侧,故不正确;
∴②和③正确.
故选B. 下面几组条件中,能判断一个四边形是平行四边形的是( )
A.一组对边相等 B.两条对角线互相平分
C.一组对边平行 D.两条对角线互相垂直
 B
【解析】
试题分析:平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.根据平行四边形的判定方法,采用排除法,逐项分析判断.
【解析】
A、一组对边相等,不能判断,故错误;
...
B
【解析】
试题分析:平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.根据平行四边形的判定方法,采用排除法,逐项分析判断.
【解析】
A、一组对边相等,不能判断,故错误;
... 计算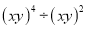 的结果是( )
的结果是( )
A. 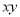 B.
B. 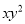 C.
C. 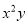 D.
D. 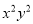
 D
【解析】试题解析: ,故答案是D选项.
故选D.
D
【解析】试题解析: ,故答案是D选项.
故选D.