题目内容
1.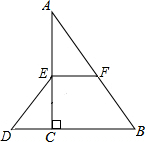 如图,在Rt△ABC中,∠ACB=90°,点E,F分别是边AC,AB的中点,延长BC到点D,使2CD=BC,连接DE.
如图,在Rt△ABC中,∠ACB=90°,点E,F分别是边AC,AB的中点,延长BC到点D,使2CD=BC,连接DE.(1)如果AB=10,求DE的长;
(2)延长DE交AF于点M,求证:点M是AF的中点.
分析 (1)连接CF,根据直角三角形的性质得到CF=$\frac{1}{2}$AB=5,根据三角形中位线定理得到EF∥BC,EF=$\frac{1}{2}$BC,证明四边形EDCF是平行四边形,根据平行四边形的性质证明;
(2)根据平行四边形的性质、平行线等分线段定理证明.
解答 解:(1)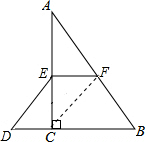 连接CF,
连接CF,
在Rt△ABC中,F是AB的中点,
∴CF=$\frac{1}{2}$AB=5,
∵点E,F分别是边AC,AB的中点,
∴EF∥BC,EF=$\frac{1}{2}$BC,
∵2CD=BC,
∴EF=CD,EF∥CD,
∴四边形EDCF是平行四边形,
∴DE=CF=5;
(2)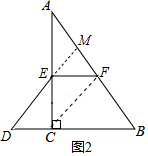 如图2,∵四边形EDCF是平行四边形,
如图2,∵四边形EDCF是平行四边形,
∴CF∥DM,
∵点E是边AC的中点,
∴点M是AF的中点.
点评 本题考查的是三角形中位线定理、平行四边形的判定和性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
9.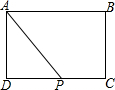 如图,在长方形ABCD中,AB=6,AD=4,点P是CD上的动点,且不与点C,D重合,设DP=x,梯形ABCP的面积为y,则下面表述正确的是( )
如图,在长方形ABCD中,AB=6,AD=4,点P是CD上的动点,且不与点C,D重合,设DP=x,梯形ABCP的面积为y,则下面表述正确的是( )
 如图,在长方形ABCD中,AB=6,AD=4,点P是CD上的动点,且不与点C,D重合,设DP=x,梯形ABCP的面积为y,则下面表述正确的是( )
如图,在长方形ABCD中,AB=6,AD=4,点P是CD上的动点,且不与点C,D重合,设DP=x,梯形ABCP的面积为y,则下面表述正确的是( )| A. | y=24-2x,0<x<6 | B. | y=24-2x,0<x<4 | C. | y=24-3x,0<x<6 | D. | y=24-3x,0<x<4 |
16.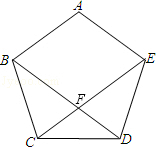 如图,正五边形ABCDE的对角线BD、CE相交于点F,则下列结论正确的是( )
如图,正五边形ABCDE的对角线BD、CE相交于点F,则下列结论正确的是( )
 如图,正五边形ABCDE的对角线BD、CE相交于点F,则下列结论正确的是( )
如图,正五边形ABCDE的对角线BD、CE相交于点F,则下列结论正确的是( )| A. | ∠BCE=36° | B. | △BCF是直角三角形 | ||
| C. | △BCD≌△CDE | D. | AB⊥BD |
13.如图,P为∠AOB内一点,OC=m(m为正数),过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.C为射线OA上任一点,连结CP并延长交OB于N点

(1)若∠AOB=60°,OQ:OM:MC=1:4:2,探索CN、ON、OC之间的数量关系并加以证明.
(2)当点P在边∠AOB的平分线上运动时,问:$\frac{1}{OM}$-$\frac{1}{ON}$的值是否发生变化?如果变化,指出该值随m的变化情况;如果不变,请说明理由.
(3)在(2)的条件下,二次函数y=ax2+bx+c的x与y的部分对应值如下表:
若m的值是关于x的方程ax2+(b-1)x+c=0中较大的根,菱形OMPQ的面积为S1,△NOC的面积为S2,求$\frac{{S}_{1}}{{S}_{2}}$的取值范围.

(1)若∠AOB=60°,OQ:OM:MC=1:4:2,探索CN、ON、OC之间的数量关系并加以证明.
(2)当点P在边∠AOB的平分线上运动时,问:$\frac{1}{OM}$-$\frac{1}{ON}$的值是否发生变化?如果变化,指出该值随m的变化情况;如果不变,请说明理由.
(3)在(2)的条件下,二次函数y=ax2+bx+c的x与y的部分对应值如下表:
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -1 | 3 | 5 | 5 | … |
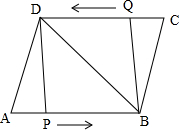 如图,已知?ABCD中,AD=8cm,AB=10cm,BD=12cm,点P从点A出发,以1cm/s的速度向点B运动,同时点Q从点C出发以相同的速度向点D运动,设运动时间为t.
如图,已知?ABCD中,AD=8cm,AB=10cm,BD=12cm,点P从点A出发,以1cm/s的速度向点B运动,同时点Q从点C出发以相同的速度向点D运动,设运动时间为t.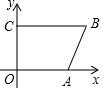 在平面直角坐标系中,A(a,0),B(12,b),C(0,b)且$\sqrt{\frac{1}{2}a-4}$+(b-6)2=0,线段PQ=7.
在平面直角坐标系中,A(a,0),B(12,b),C(0,b)且$\sqrt{\frac{1}{2}a-4}$+(b-6)2=0,线段PQ=7.