题目内容
3.小明研究了以下一种二叉图形的结点( )数,如图,一层二叉树的结点总数为1,二层二叉树的点总数为3,三层二叉树的结点总数为7,…照此规律,你认为八层二叉树的结点总数为( )
)数,如图,一层二叉树的结点总数为1,二层二叉树的点总数为3,三层二叉树的结点总数为7,…照此规律,你认为八层二叉树的结点总数为( )
| A. | 127 | B. | 168 | C. | 255 | D. | 512 |
分析 观察图形可知每增加一层,二叉树的结点总数会比前一个多出2n-1个,而n层二叉树的结点总数为1+2+22+23+…+2 n-1是一个等比数列的和,即$\frac{1×(1-{2}^{n})}{1-2}$=2n-1,再把n=8代入即可求解.
解答 解:由图可知
一层二叉树的结点总数为1,
二层二叉树的点总数为3=1+2
三层二叉树的结点总数为7=1+2+4=1+2+22,
四层二叉树的结点总数为1+2+22+23,
…
n层二叉树的结点总数为1+2+22+23+…+2 n-1=$\frac{1×(1-{2}^{n})}{1-2}$=2n-1
所以八层二叉树的结点总数为:28-1=255
故答案为:C
点评 本题主要考查了图形的变化规律,解本题的关键是根据图形的变化规律发现每增加一层,二叉树的结点总数会比前一个多出2n-1个,从而得到一个等比数列.先找到一般方法再代入特殊值求解.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
8. 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )
 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )| A. | 70° | B. | 90° | C. | 110° | D. | 120° |
15.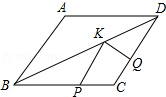 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
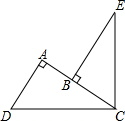 如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.
如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.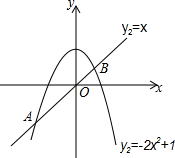 如图,抛物线y1=-2x2+1和直线y2=x交于A、B两点.
如图,抛物线y1=-2x2+1和直线y2=x交于A、B两点.