题目内容
18.如图,用火柴棒按下列方式搭三角形,照这样搭下去:
(1)搭5个这样的三角形需要11根火柴棒.
(2)搭n个这样的三角形需要1+2n根火柴棒.
(3)通过计算,并回答搭2010个这样的三角形需要多少根火柴棒?
分析 通过观察图形的变化可得:每增加一个三角形就会增加2根火柴,按照这个规律搭下去,火柴的总数是一个等差数列的和.先根据规律求出第五个图形中的火柴棒是1+2×5=11根,再求出一般规律为1+2n,最后把n=2010代入一般规律即可求解.
解答 解:观察图形可知
第一个图共有火柴棒1+2=1+2×1=3根,
第二个图共有火柴棒1+2+2=1+2×2=5根,
第三个图共有火柴棒1+2+2+2=1+2×3=7根,
第四个图共有火柴棒1+2+2+2+2=1+2×4=9根,
第五个图共有火柴棒1+2+2+2+2+2=1+2×5=11根,
…
第n个图共有火柴棒(1+2n)根.
当n=2010时,1+2n=1+2×2010=4021,
即搭2010个这样的三角形需要4021根火柴棒
故答案为:(1)11;(2)1+2n(3)搭2010个这样的三角形需要40;21根火柴棒.
点评 本题主要考查了如何从变化的图形中找规律,并用规律解题.注意本题中主要是根据火柴的总数是一个等差数列的和来得到一般规律.要把变化的数据分成不变的量和变化的量两个部分,把变化的部分与图形的序号找出对应关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.若x表示一个两位数,把数字3放在x的右边,组成一个三位数是( )
| A. | 3x | B. | 10x+3 | C. | 100x+3 | D. | 3×100+x |
3.小明研究了以下一种二叉图形的结点( )数,如图,一层二叉树的结点总数为1,二层二叉树的点总数为3,三层二叉树的结点总数为7,…照此规律,你认为八层二叉树的结点总数为( )
)数,如图,一层二叉树的结点总数为1,二层二叉树的点总数为3,三层二叉树的结点总数为7,…照此规律,你认为八层二叉树的结点总数为( )

 )数,如图,一层二叉树的结点总数为1,二层二叉树的点总数为3,三层二叉树的结点总数为7,…照此规律,你认为八层二叉树的结点总数为( )
)数,如图,一层二叉树的结点总数为1,二层二叉树的点总数为3,三层二叉树的结点总数为7,…照此规律,你认为八层二叉树的结点总数为( )
| A. | 127 | B. | 168 | C. | 255 | D. | 512 |
8.下列命题是假命题是( )
| A. | 三角形两边的差小于第三边 | |
| B. | 凸多边形的外角和都等于360° | |
| C. | 凸五边形共有4条对角线 | |
| D. | 三角形三条中线的交点是三角形的重心 |
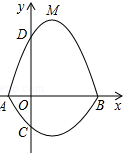 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
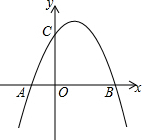 如图,已知c>0,抛物线y=-x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.
如图,已知c>0,抛物线y=-x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C. 如图所示,AB+CD<AC+BD.(填“<”,“>”或“=”)
如图所示,AB+CD<AC+BD.(填“<”,“>”或“=”)